Алгоритмическое обеспечение робастных асимптотических наблюдателей производных

В.Х. Пшихопов; М.Ю.Медведев

Алгоритмическое обеспечение робастных асимптотических наблюдателей производных

Аннотация

В.Х. Пшихопов, М.Ю.Медведев

В работе развивается алгоритмическое обеспечение асимптотических наблюдателей производных, используемых в адаптивных системах управления. На базе принципа максимума предлагается метод структурного синтеза наблюдателя, состоящего из цепочки блоков, каждый из которых оценивает одну производную. Показано, что выбор вспомогательных переменных на основе ошибки оценивания приводит в ограниченной области пространства состояния к субоптимальным по быстродействию решениям. Приводятся результаты компьютерного моделирования, подтверждающие теоретические выкладки.
Ключевые слова: асимптотическое оценивание, робастность, принцип максимума.

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Введение
Наиболее полная информация об оцениваемом процессе содержится в его математической модели, поэтому в теории управления широкое распространение получили методы оценивания, основанные на использовании дифференциальных уравнений, описывающих объект. Как известно, оптимальное решение задачи оценивания получено для линейных систем и представляет собой фильтр Калмана – Бьюси [1]. Однако при наличии неопределенностей требуется адаптация к модели объекта, параметрам шумов и действующим на систему возмущениям. Кроме того, недостатком фильтра Калмана-Бьюси является тот факт, что его коэффициенты передачи вычисляются в разомкнутой форме как решения уравнения Риккати при заданных математических ожиданиях начальных условий оцениваемого процесса и ковариационной матрицы. Это ухудшает свойства фильтра при действии неучтенных факторов.
В работах [2 – 4] рассматриваются различные варианты аппроксимирующих наблюдателей, использующих разложение оцениваемого процесса во временные ряды. В [2] предложено в дискретные моменты времени корректировать коэффициенты усиления, полученные в результате решения уравнения Риккати, в соответствие с текущей ошибкой оценивания. Однако, дискретное корректирование коэффициентов усиления фильтра приводит к дополнительным переходным процессам, поэтому оценки таким способом можно получать только в определенные моменты времени. В [3] используется аналогичный наблюдатель, названный рекуррентным наблюдателем производных (РНП), позволяющий оценивать возмущения и фазовые переменные системы, коэффициенты которого выбираются из требуемых условий подавления шумов. При этом предложены специальная каскадная структура наблюдателя и нелинейное изменение коэффициентов усиления, обеспечивающее повышение быстродействия наблюдателя. В работе [4] предлагается наблюдатель, коэффициенты усиления которого непрерывно зависят от ошибки оценивания, при стремлении ошибки оценивания к нулю сходятся к постоянным значениям. В данной статье предлагается новый метод синтеза нелинейных наблюдателей, отличительной особенностью которого является то, что он обеспечивает синтез структуры наблюдателя. Метод основа на подходе, изложенном в работах [5, 6]. Предлагаемые алгоритмы могут использоваться в системах управления [7], для которых нет необходимости точно измерять производные, а достаточно асимптотической сходимости получаемых оценок.
Процедура синтеза наблюдателя
При синтезе РНП [3, 4] структура и изменение коэффициентов усиления выбираются так, что их качественное изменение соответствует фильтру Калмана-Бьюси, т.е. в области больших отклонений коэффициенты усиления принимают большие значения, а в области малых отклонений – уменьшаются. Однако фильтр Калмана-Бьюси минимизирует среднеквадратичную ошибку оценивания при наличии измерительного шума и случайных начальных условиях объекта. Рассмотрим ситуацию, когда требуется синтезировать наблюдатель, осуществляющий оценивание наибыстрейшим образом при заданном уровне подавления шумов.
Иными словами ставится задача синтеза рекуррентного наблюдателя производных по критерию быстродействия при ограничениях, задаваемых требуемым качеством подавления шумов. Для синтеза такого наблюдателя используются два положения. Первое заключается в применении локальной (скользящей) аппроксимации временным рядом, которая может быть представлена в виде цепочки последовательно включенных динамических звеньев, описываемых уравнениями [3, 4]: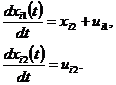
(1)
где – некоторые функции, структура и параметры которых подлежат выбору в процессе синтеза.
В исходных уравнениях РНП [3, 4] функции априорно заданы в виде линейных функций ошибки оценивания наблюдаемой величины
    (2)
где – постоянные коэффициенты усиления, – входная переменная блока наблюдателя.
В настоящей работе для выбора функций используется метод, предложенный в [5 – 7], основанный на принципе максимума Понтрягина. Новизна данного метода состоит в новой процедуре конструирования функции Понтрягина при использовании принципа максимума в форме динамического программирования. При этом вектор вспомогательных переменных строится на основе ошибки регулирования, что обеспечивает высокую робастность получаемых законов управления. С другой стороны, такой способ построения функции Понтрягина не позволяет сделать ее постоянной, т.е. ее положительность необходимо проверять в момент переключения. В этой связи требуется заменять функцию «сигнум» на некоторую непрерывную функцию, т.е. переходить от оптимального к субоптимальному решению.
Основной целью наблюдателя (1) является сведение к нулю ошибки оценивания. В этом случае цель синтеза может быть сформулирована в виде следующего многообразия:
.    (3)
В соответствии с работами [5 – 7] сформируем следующую функцию Понтрягина:
. (4)
Управляющие воздействия , определяющие структуру и параметры наблюдателя, входят в выражение (4) линейно, поэтому максимум функции Понтрягина достигается на ограничениях:
(5)
,    (6)
где , – ограничения на управляющие воздействия.
Подстановка выражений (5), (6) в (4) дает следующее выражение для функции Понтрягина замкнутой системы:
.    (7)
Из (7) видно, что при выполнении условия
,     (8)
функция Понтрягина (7) наблюдателя (1), (5), (6) является положительно определенной.
Легко проверить, что во всех точках непрерывности функция Понтрягина (7) удовлетворяет выражениям:
,   (9)
.      (10)
Таким образом, изменение коэффициентов усиления наблюдателя (1) в соответствие с выражениями (5), (6) обеспечивают выполнение условий, аналогичных условиям принципа максимума Понтрягина. Отметим, что в результате синтеза получена структура наблюдателя. Его параметры , могут определяться исходя из требований к подавлению шумов. Например, если в выражениях (5), (6) исключить знаковую функцию, то получим линейный наблюдатель. В этом случае параметры , можно найти в соответствии методикой, изложенной в [4].
Аппроксимация релейных коэффициентов усиления
Выражения (9), (10) не могут рассматриваться в моменты переключения функций (5), (6). В этой связи необходимо осуществлять аппроксимацию релейных переключений непрерывными функциями и говорить о субоптимальном по быстродействию оценивании.
Кроме того, релейные управления приводят к системам дифференциальных уравнений с разрывными правыми частями, что может стать причиной наличия автоколебаний. Кроме того, релейные управления требуют мгновенных переключений управляющих воздействий, что на практике реализуется только приближенно.
Таким образом, задача аппроксимации релейных законов непрерывными функциями, обусловленная тремя факторами:
– невозможностью практической реализации мгновенных изменений физических величин;
– неустойчивостью в малом релейных систем управления;
– математической некорректностью, связанной с не единственностью решений дифференциальных уравнений с разрывными правыми частями.
При решении аппроксимации релейных управлений важны следующие критерии:
– близость непрерывной функции к релейной;
– обеспечение асимптотической устойчивости системы;
– решение задачи жесткости системы для вычислительных процедур.
Последний критерий связан с тем, что процессы в реальных объектах протекают относительно медленно, а управляющие воздействия в релейных системах изменяются намного быстрее. Это приводит к наличию в системе «медленных» и «быстрых» переменных, что обуславливает жесткость решаемой задачи с точки зрения вычислительной сложности.
В настоящее время для аппроксимации релейных управлений используется несколько непрерывных функций, свойства которых хорошо изучены. Например, в нейросетях широко используется функция сигмоидального тангенса:
,    (11)
где – параметр, определяющий близость непрерывной функции (11) к знаковой функции .
Данная функция похожа на гиперболический тангенс, однако отличается лучшими свойствами для вычислительных процедур.
Моделирование наблюдателя
Рассмотрим результаты сравнительного моделирования линейного и оптимального по быстродействию наблюдателей, представленные на рис. 1 – 4.

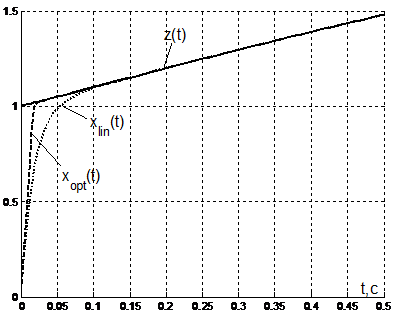
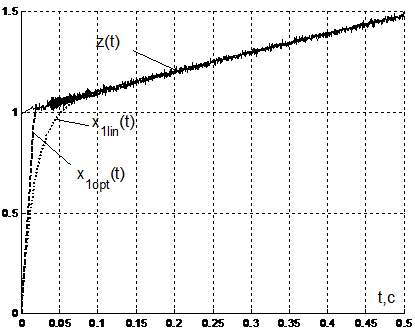
Рисунок 1 – Входная переменная z(t) и ее асимптотические оценки: линейная xlin(t) и субоптимальная xopt(t)

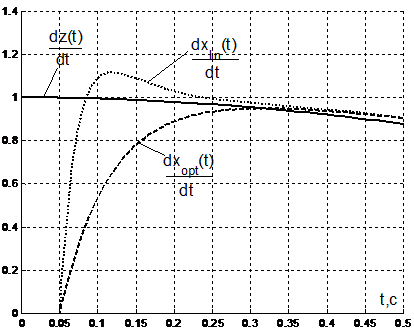
Рисунок 2 – Первая производная и ее асимптотические оценки: линейная и субоптимальная

Коэффициенты передачи линейного наблюдателя описываются выражениями (2), а робастного субоптимального наблюдателя – выражениями (5), (6).
При моделировании входной сигнал задается следующей функцией времени
.
Ограничения на управляющие воздействия заданы в виде:
.
В линейном наблюдателе коэффициенты усиления равны:
.
При моделировании оптимального РНП знаковая функция заменена на близкую непрерывную функцию , которая широко используется в функциях активации нейросетей.

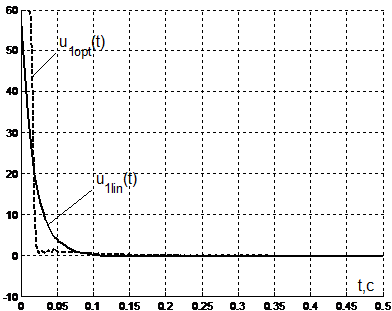Рисунок 3 – Изменение первого управляющего воздействия в линейном и субоптимальном наблюдателях

Из результатов моделирования, представленных на рис. 1 и 2 видно, что оценивание в оптимальном по быстродействию наблюдателе происходит заметно быстрее. При этом, сравнивая изменение управляющих воздействий в наблюдателях, представленные на рис. 3 и 4, можно увидеть, что в области больших отклонений управляющие воздействия в оптимальном по быстродействию наблюдателе превосходят управляющие воздействия в линейном наблюдателе. Однако, в области малых отклонений, которая ограниченная моментами переключения управляющих воздействий в оптимальной системе, коэффициенты усиления последней близки к нулю. В этой связи в области малых отклонений можно переключаться на линейный алгоритм оценивания. При этом важным фактором является возможность для субоптимального РНП определить момент достижения «области малых отклонений», как момент переключения управляющих воздействий.

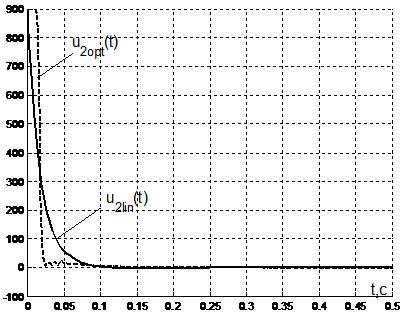Рисунок 4 – Изменение второго управляющего воздействия в линейном и субоптимальном наблюдателях

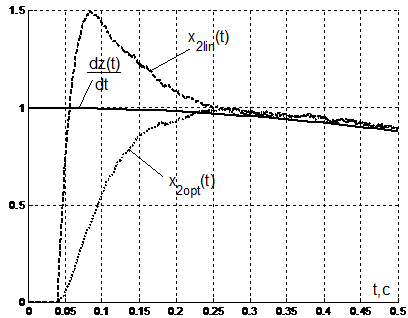
На рис. 5 и 6 приведены результаты моделирования линейного и субоптимального наблюдателей при действии случайных измерительных шумов. Из рис. 5 и 6 можно сделать вывод, что наличие шума не влияет на выводы, сделанные выше.

Рисунок 5 – Оценивание выходной переменной линейным и субоптимальным наблюдателями при наличии случайного измерительного шума

Рисунок 6 – Оценивание производной выходной переменной линейным и субоптимальным наблюдателями при наличии случайного шума

Заключение
В данной статье представлен новый метод синтеза асимптотических наблюдателей производных, обеспечивающих максимальное быстродействие при заданной степени подавления шумов. Наблюдатель синтезирован на основе принципа максимума, в результате применения которого получена его структура и параметры. Изложенный метод может быть использован для синтеза наблюдателей в системах произвольно структуры, в том числе для нелинейных систем.

Литература