Программный комплекс τ-полнота (B, S)-рынка в случае специальной хааровской фильтрации при допущении арбитража.
Аннотация
Рассматривается программный комплекс Τ-полноты (В,S)-рынка относительно специальной хааровской фильтрации.
Ключевые слова: полнота,τ-полнота, арбитраж, (B,S)-рынок
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Рассматриваемый программный комплекс предоставляет возможность пользователю задать компоненты 
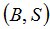 -рынка относительно специальной хааровской фильтрации посредством ввода конечного момента времени
-рынка относительно специальной хааровской фильтрации посредством ввода конечного момента времени 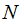 , последовательности строго положительных цен банковского счёта
, последовательности строго положительных цен банковского счёта 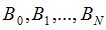 и последовательности строго положительных цен акций в моменты времени
и последовательности строго положительных цен акций в моменты времени 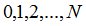 . Далее предоставляется возможность ввода случайной величины
. Далее предоставляется возможность ввода случайной величины 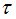 на атомах
на атомах 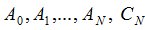 , определяющих рынок в конечный момент времени.
, определяющих рынок в конечный момент времени.
Так начинает свою работу основная программа, переходящая в последовательное выполнение процедур MO, MATR, MGAUS, HEDG, описанных ниже.
Процедура MO находит 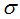 -алгебру
-алгебру 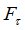 , совпадающую с одной из
, совпадающую с одной из 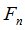 ,
, 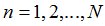 в случае, если случайная величина
в случае, если случайная величина 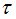 является моментом остановки. Теоретическая база, положенная в основу факта совпадения
является моментом остановки. Теоретическая база, положенная в основу факта совпадения 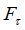 с одной из
с одной из 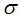 -алгебр
-алгебр 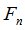 ,
, 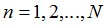 изложена в лемме 3[1]. Поиск номера
изложена в лемме 3[1]. Поиск номера 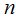 осуществляется по алгоритму, опирающемуся на лемму 1[1] и следствие леммы 2[1]. Здесь также предусмотрена возможность завершения программы в случае, когда случайная величина
осуществляется по алгоритму, опирающемуся на лемму 1[1] и следствие леммы 2[1]. Здесь также предусмотрена возможность завершения программы в случае, когда случайная величина 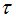 не является моментом остановки.
не является моментом остановки.
Процедура MATR путём перехода к 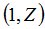 -рынку[2] формирует матрицу коэффициентов
-рынку[2] формирует матрицу коэффициентов 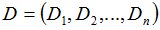 размером
размером 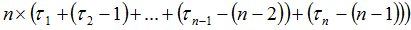 , состоящую из
, состоящую из 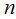 матриц вида
матриц вида
 ,
,
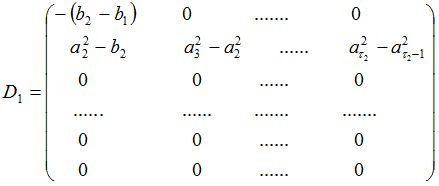 ,
,
…………………………………………….....
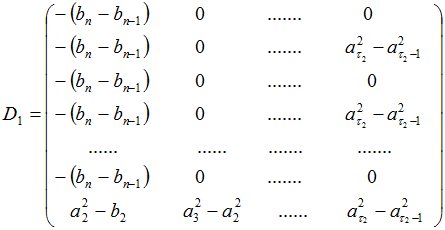
Ранг матрицы 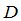 отвечает за полноту рассматриваемого рынка[1]. Процедура MGAUS осуществляет элементарные преобразования над матрицей
отвечает за полноту рассматриваемого рынка[1]. Процедура MGAUS осуществляет элементарные преобразования над матрицей 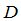 , приводя её к виду, при котором первые
, приводя её к виду, при котором первые 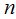 столбцов матрицы имеют единичный вид.. Процедура опирается на общеизвестный факт, говорящий о том, что с помощью конечного числа элементарных преобразований любую матрицу можно привести к ступенчатому виду. В [1] доказано, что рынок полон по отношению к моменту времени
столбцов матрицы имеют единичный вид.. Процедура опирается на общеизвестный факт, говорящий о том, что с помощью конечного числа элементарных преобразований любую матрицу можно привести к ступенчатому виду. В [1] доказано, что рынок полон по отношению к моменту времени 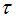 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 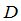 имеет ранг, равный
имеет ранг, равный 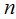 .
.
Далее путём подсчёта ненулевых строк матрицы 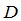 определяется её ранг, что позволяет сделать вывод о
определяется её ранг, что позволяет сделать вывод о 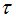 -полноте рынка. В случае отсутствия
-полноте рынка. В случае отсутствия 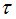 -полноты работа программы завершается.
-полноты работа программы завершается.
В случае наличия 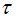 -полноты пользователю предоставляется возможность ввести компоненты финансового обязательства а атомах
-полноты пользователю предоставляется возможность ввести компоненты финансового обязательства а атомах 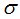 -алгебры
-алгебры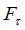 . Процедура HEDG подсчитывает компоненты самофинансируемого портфеля
. Процедура HEDG подсчитывает компоненты самофинансируемого портфеля 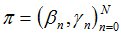 , реплицирующего заданное финансовое обязательство.
, реплицирующего заданное финансовое обязательство.
Рассмотрим работу программы на примере.
Пример. Рассмотрим стохастический базис 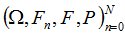 ,
, 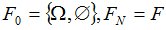 и
и 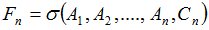 , причём
, причём 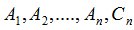 - полный набор атомов
- полный набор атомов 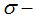 алгебры
алгебры 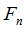 .
.
Такая фильтрация называется специальной хааровской[3].
Положим 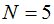 и зададим последовательность цен банковского счёта
и зададим последовательность цен банковского счёта 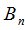 и последовательность цен акций акций
и последовательность цен акций акций 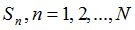 на атомах
на атомах 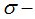 алгебр
алгебр 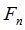 в различные моменты времени:
в различные моменты времени:
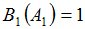 |
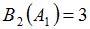 |
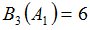 |
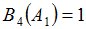 |
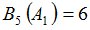 |
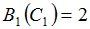 |
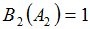 |
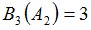 |
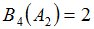 |
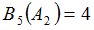 |
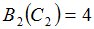 |
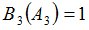 |
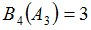 |
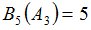 |
|
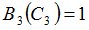 |
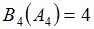 |
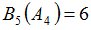 |
||
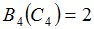 |
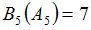 |
|||
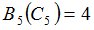 |
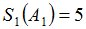 |
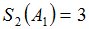 |
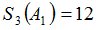 |
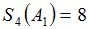 |
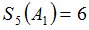 |
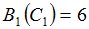 |
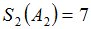 |
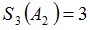 |
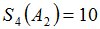 |
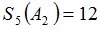 |
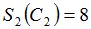 |
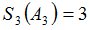 |
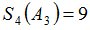 |
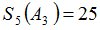 |
|
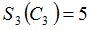 |
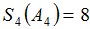 |
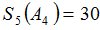 |
||
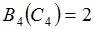 |
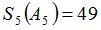 |
|||
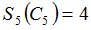 |
Зададим также случайную величину 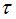 :
:
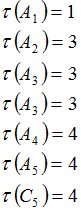
Процедура MO определит, что случайная величина 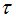 является моментом остановки и
является моментом остановки и 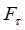 совпадает с
совпадает с 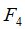 .
.
Процедура MATR осуществит переход к 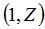 -рынку[2]:
-рынку[2]:
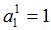 |
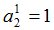 |
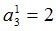 |
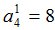 |
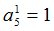 |
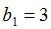 |
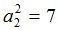 |
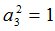 |
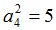 |
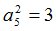 |
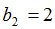 |
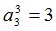 |
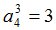 |
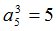 |
|
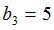 |
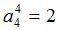 |
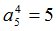 |
||
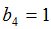 |
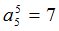 |
|||
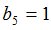 |
Далее будет сформирована матрица 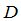 :
:
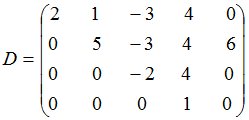
Процедура MGAUS приведёт матрицу D к виду

Здесь определится, что ранг матрицы равен 4, то есть она имеет полный ранг. Выдаётся сообщение о полноте относительно 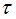 .
.
Процедура HEDG предлагает задать компоненты финансового обязательства на атомах 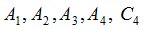
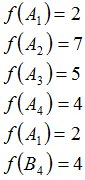
Подсчитываются компоненты самофинансируемого портфеля 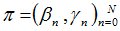 , реплицирующего данное финансовое обязательство
, реплицирующего данное финансовое обязательство
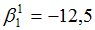 |
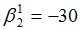 |
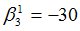 |
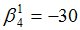 |
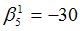 |
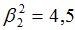 |
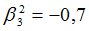 |
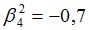 |
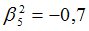 |
|
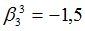 |
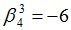 |
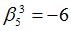 |
||
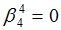 |
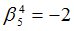 |
|||
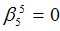 |
||||
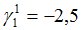 |
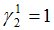 |
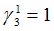 |
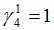 |
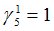 |
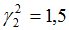 |
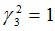 |
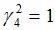 |
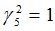 |
|
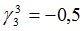 |
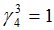 |
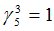 |
||
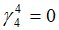 |
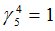 |
|||
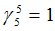 |
Литература
1. Шишкова А.Н. Критерий 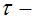 полноты -рынка в случае специальной хааровской фильтрации при допущении арбитража // Известия высших учебных заведений: Северо-Кавказский регион, 2010, №4-c.24-27.
полноты -рынка в случае специальной хааровской фильтрации при допущении арбитража // Известия высших учебных заведений: Северо-Кавказский регион, 2010, №4-c.24-27.
2. Белявский Г.И., Мисюра В.В., Павлов И.В. Ранговый критерий полноты одного арбитражного рынка при допущении арбитража.// ОППМ, М: ТВП, 1999, т.6, №1, с.121122.
3. Волосатова Т.А. О хааровских интерполяциях финансовых рынков, приводящих к полным рынкам. ОППМ, М: ТВП, 2004, т. 11, №.3, с. 505-506.