Моделирование сбоев и их устранение на финансовых рынках с потоком событий, порожденным бинарным деревом
Аннотация
Дата поступления статьи: 30.10.2013Рассматривается дисконтированный финансовый рынок на стохастическом базисе с фильтрацией, порожденной бинарным деревом. Построен программный модуль, моделирующий сбои на этом рынке. Под сбоем понимается такая ситуация на финансовом рынке, когда при переходе от предыдущего момента времени к последующему новые события возникают, однако дисконтированная цена акции (какого-то фиксированного типа) не изменяется. Сбой порождает неполноту рынка (множество мартингальных мер этого рынка бесконечно). Посредством моделирования слабой деформации удается свести множество мартингальных мер к одной мартингальной мере. Тем самым единственным образом определяется цена любого платежного обязательства, которую в определенном смысле можно считать "справедливой ценой".
Ключевые слова: Стохастический базис, вероятностная мера, финансовый рынок, бинарное дерево, безарбитражность, полнота, слабая деформация, мартингальная мера, программный модуль.
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Рассмотрим стохастический базис ![]() , где
, где ![]() — конечное множество исходов на некотором финансовом рынке;
— конечное множество исходов на некотором финансовом рынке; ![]() —
— ![]() -алгебра событий на этом рынке, доступных для наблюдения до момента времени
-алгебра событий на этом рынке, доступных для наблюдения до момента времени ![]() включительно;
включительно; ![]() — вероятностная мера, нагружающая все атомы финальной
— вероятностная мера, нагружающая все атомы финальной ![]() -алгебры
-алгебры ![]() .
.
Определение.Под сбоем понимается такая ситуация на рынке акций, когда при временной эволюции рынка новые события возникают, однако дисконтированная цена акции (какого-то фиксированного типа) не изменяется.
Например, пусть ![]() — адаптированный случайный процесс, представляющий собой эволюцию дисконтированной цены акции определенного типа, и атом
— адаптированный случайный процесс, представляющий собой эволюцию дисконтированной цены акции определенного типа, и атом ![]()
![]() -алгебры
-алгебры ![]() таков, что
таков, что ![]() , где
, где ![]() и
и ![]() есть атомы
есть атомы ![]() -алгебры
-алгебры ![]() . Если выполняется равенство
. Если выполняется равенство ![]() , то это и означает, что в момент времени
, то это и означает, что в момент времени ![]() на атоме
на атоме ![]() произошел сбой.
произошел сбой.
В работах [1,2] было доказано, что отсутствие сбоя равносильно интерполяционному свойству финансового рынка, названному свойством хааровской единственности (СХЕ). Из этого результата вытекает, что при наличии хотя бы одного сбоя неполный и безарбитражный финансовый рынок не может быть преобразован посредством хааровской интерполяции в полный и безарбитражный рынок.
Настоящая статья посвящена моделированию сбоев на финансовых рынках с потоком событий, порожденным бинарным деревом (важность такой модели демонстрирует монография [3] и работы [4–6]). В ней описывается работа одного из модулей созданного авторами программного комплекса. Основная цель работы — показать, что переходом от исходной (физической) вероятностной меры ![]() к эквивалентной ей слабой деформации
к эквивалентной ей слабой деформации ![]() можно «исправить» рынок со сбоем таким образом, что он будет обладать единственной строго эквивалентной деформации
можно «исправить» рынок со сбоем таким образом, что он будет обладать единственной строго эквивалентной деформации ![]() мартингальной деформацией (терминология разъясняется в [7]). Сбои можно моделировать и на других рынках (см. [8-9]). Относительно применений см. также [10].
мартингальной деформацией (терминология разъясняется в [7]). Сбои можно моделировать и на других рынках (см. [8-9]). Относительно применений см. также [10].
В программном комплексе реализовано автоматическое моделирование сбоев. Допущения: 1) количество сбоев в любой момент времени ограничено сверху числом ![]() (
(![]() задается в зависимости от конкретной задачи); 2) могут существовать моменты времени, в которых
задается в зависимости от конкретной задачи); 2) могут существовать моменты времени, в которых ![]() (нет сбоев) 3) на атомах
(нет сбоев) 3) на атомах ![]() и
и ![]() , возникших после сбоя, плотность
, возникших после сбоя, плотность ![]() деформации задается равенствами
деформации задается равенствами ![]() и
и ![]() . Если
. Если ![]() мыслится как случайная величина с областью значений в интервале
мыслится как случайная величина с областью значений в интервале ![]() , то ее значение при каждом сбое моделируется заново. В частном случае, если
, то ее значение при каждом сбое моделируется заново. В частном случае, если ![]() , эта константа едина для всех сбоев.
, эта константа едина для всех сбоев.
Имитационное моделирование сбоев осуществляется в соответствии со следующим алгоритмом.
1. В рамках рассматриваемой модели сбой может произойти в каждый момент времени с заданной заранее фиксированной вероятностью ![]() .
.
2. Если в какой-то момент времени сбой происходит, то моделирование его величины производится на случайным образом выбранном атоме. Если при этом ![]() , то случайным образом отбираются еще
, то случайным образом отбираются еще ![]() атомов и каждый из этих атомов экзаменуется на наличие сбоя (вероятность наличия сбоя на каждом из этих атомов обозначается
атомов и каждый из этих атомов экзаменуется на наличие сбоя (вероятность наличия сбоя на каждом из этих атомов обозначается ![]() ).
).
3. После сбоя цена акции опять ведет себя в соответствии с исходными параметрами ее эволюции.
Описанная выше процедура реализована в виде плагина, который в случае надобности подключается к основной программе. В следующем примере сбои моделируются в рамках классической CRR-модели (модели Кокса-Росса-Рубинштейна).
Пример. Создадим CRR-модель с параметрами, приведенными на рисунке 1 (буквы ![]() и
и ![]() стандартным образом отражают случайную процентную ставку по акции, а буква
стандартным образом отражают случайную процентную ставку по акции, а буква ![]() — процентную ставку банковского счета). Так как
— процентную ставку банковского счета). Так как ![]() , то выбран дисконтированный рынок.
, то выбран дисконтированный рынок.

Рис. 1. Параметры CRR-модели
Созданное программой дерево модели показано на рисунке 2.
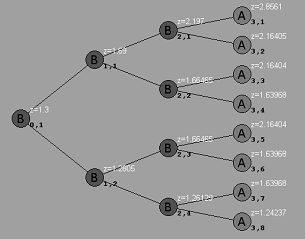
Рис. 2. Дерево модели
Если в какой-то момент времени в модели возникает сбой, то в результате полная и безарбитражная модель финансового рынка превращается в неполную. Сбой моделируется с параметрами, указанными на рис. 3, где ![]() , а
, а ![]() (см. пункт 2 алгоритма).
(см. пункт 2 алгоритма).
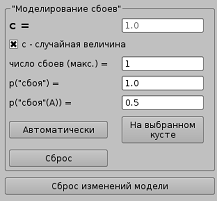
Рис. 3. Параметры моделирования сбоев
В результате получаем процесс эволюции цены акции со сбоями (нижний индекс — временной, а верхний указывает номер атома): ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() . Получили неполный рынок.
. Получили неполный рынок.
Для выбора типа платежного обязательства предназначена специальная панель. С ее помощью задаем ![]() как опцион продажи при цене поставки цену
как опцион продажи при цене поставки цену![]() . А именно,
. А именно, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Применяя технику мартингальных деформаций, можно вычислить полный капитал самофинансируемого портфеля. Вычисления показывают, что аналог справедливой цены выбранного платежного обязательства
. Применяя технику мартингальных деформаций, можно вычислить полный капитал самофинансируемого портфеля. Вычисления показывают, что аналог справедливой цены выбранного платежного обязательства ![]() равен 1,7.
равен 1,7.
Метод хааровских интерполяций, разработанный в [1,2], к сожалению, не позволяет интерполировать построенный рынок до полного и рассчитать соответствующий совершенный хедж.
Данная работа выполнена при поддержке РФФИ, грант № 13-01-00637а
Литература:
- Богачева М.Н., Павлов И.В. О хааровских расширениях безарбитражных финансовых рынков до безарбитражных и полных [Текст] // УМН, 2002. – Т. 57. – Вып. 3. – С. 143-144.
- Богачева М.Н., Павлов И.В. О хааровских расширениях безарбитражных финансовых рынков до безарбитражных и полных [Текст] // Известия вузов. Северо-Кавказский регион. Естественные науки, 2002. – №3. С. 16-24.
- Shreve S.E. Stochastic Calculus for Finance I. The Binomial Asset Pricing Model [Текст] // Springer Verlag N.Y., 2004. – 187 p.
- Schumacher N. Binomial option pricing with nonidentically distributed returns and its implications [Текст] // Mathematical and Computer Modeling, 1999. – №29. – P. 121–143.
- Detemple J., Sundaresan S. Nontraded asset valuation with portfolio constraints: a binomial approach [Текст] // The Review of Financial Stadies, 1999. – Vol. 12. – №4. – P. 835–872.
- Favero G. Shortfall risk minimization under model uncertainty in the binomial case: adaptive and robust approaches [Текст] // Math. Meth. Oper. Res., 2001. – №53. – P. 493–503.
- Назарько О.В. Слабые деформации на бинарных финансовых рынках [Текст] // Известия ВУЗов. Северо-Кавказский регион. Естественные науки, 2010. – Вып. 1. – С. 12–18.
- Назарько О.В., Павлов И.В. Рекуррентный метод построения слабых деформаций по процессу плотностей в рамках модели стохастического базиса, снабженного специальной хааровской фильтрацией [Текст] // Вестник РГУПС, 2012. – №1. – С. 200–208.
- Красий Н.П. О вычислении спрэда для обобщённой модели (B,S)-рынка в случае скупки акций [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1378 (доступ свободный). – Загл. с экрана. – Яз. рус.
- Назарько О.В., Павлов И.В., Чернов А.В. Моделирование оптимальной полосы пропускания телекоммуникационных каналов при условии гарантированной и негарантированной доставки пакетов [Электронный ресурс] // «Инженерный Вестник Дона», 2012, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2012/652 (доступ свободный). – Загл. с экрана. – Яз. рус.