К асимптотическому анализу волновых полей в слоисто-неоднородных средах

Аннотация

Р.Р. Кадыров, А.А. Ляпин

Дата поступления статьи: 28.11.2013

На основе специального представления решений уравнений движения для многослойной полуплоскости при установившихся гармонических колебаниях рассмотрено применение асимптотических методов анализа полей смещений в среде. Большим  параметром в предлагаемом методе исследования является  расстояние от источника колебания до предполагаемой точки наблюдения с учетом переотражения волн от границы раздела слоев структуры.  Приведены результаты численных расчетов и сделан вывод об эффективности предложенного метода построения асимптотического разложения. 

Ключевые слова: асимптотическое разложение, интеграл Фурье, многослойная среда

05.23.17 - Строительная механика

         Рассматривается построение асимптотических разложений волновых полей на примере задачи сдвига для упругой двухслойной полуплоскости при гармонических колебаниях. Актуальность проблемы определяется многочисленными приложениями моделей слоистых полуограниченных сред при описании динамического поведения зданий и сооружений на многослойных основаниях, слоистых композитов, конструкций дорожных одежд и др. [1-3]. В качестве большого параметра в рассматриваемом подходе выступает расстояние от источника колебания до предполагаемой точки наблюдения с учетом переотражения волн от границы раздела слоев структуры. Приведены результаты численных расчетов.
Рассмотрим процесс возбуждения и распространения установившихся гармонических колебаний в двухслойной полуплоскости, описываемой в декартовой системе координат:

;
(рис. 1)

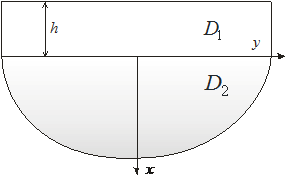
Рис. 1 .

под действием заданных на границе сдвиговых усилий:
      (1)                                 
Решение задачи в соответствии с принципом суперпозиции [4] сводится к определению трех функций напряжений, преобразованных по Фурье [5]  из граничных условий и условий сопряжения сред, что приводит к системе линейных алгебраических уравнений
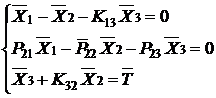     (2) .                                    
Операторы ,-алгебраические. Несложно после обращения системы (2) получить соотношения
.
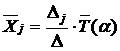При этом  и   как функции параметра   зависят также от толщины поверхностного слоя .
Функции перемещений среды восстанавливаются из интегрального представления вида [1,6]:
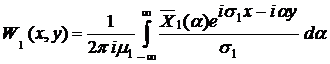 ,      .   (3)
При проведении асимптотического анализа интеграла (3) зависимость  от  накладывает ограничения на выбор параметра разложения. Для проведения такого анализа система (2) может быть решается методом последовательных приближений [7]. Для этого вводится параметр , качественно отвечающий за связь решений путем учета многократных переотражений волн от границ слоя.
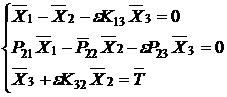  (4)                                   
Решение системы (2) можно получить из решения (4) путем предельного перехода  при .
Будем разыскивать неизвестные  по степеням :
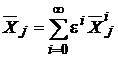     (5)                                                          
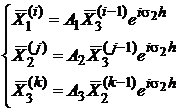
Подставляя разложение (5) в систему (4) и приравнивая слагаемые при различных степенях , получим рекуррентные соотношения 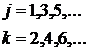(6)
                          (6)                     
,    ,      ,  .
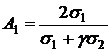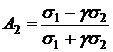Откуда имеем в явном виде



С использованием полученного представления (6) проведем асимптотический анализ интеграла (3) для поля перемещений в полуплоскости, представив функцию  в виде ряда
.
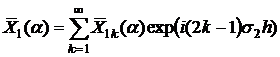Для каждого члена ряда, поменяв порядок операций интегрирования и суммирования,  применяется метод стационарной фазы. При этом  осциллирующие экспоненты  должны быть внесены в фазовую функцию.
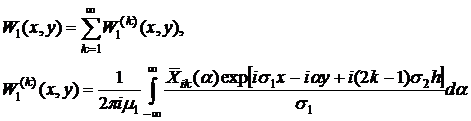  (7)               
Для каждого  показывается, что существует единственная невырожденная стационарная точка в диапазоне , для которой можно получить асимптотическую оценку по параметру   [8]. По физическому смыслу слагаемые   соответствуют цилиндрическим волнам,  раз отраженным (преломленным) от границ поверхностного слоя [9].
Отметим, что аналогично асимптотический анализ волновых полей может быть осуществлен и для точек слоя при . Однако к получаемым представлениям следует добавить вклад от поверхностных волн Лява [10].
В качестве примера на рис. 2 представлена зависимость модуля перемещений точки полуплоскости с координатами: 0.7, 0.7  при изменении толщины поверхностного слоя.  Сплошной линией нанесено точное решение, штриховой - асимптотика для тонких слоев, штрих-пунктирной - асимптотика с учетом первого переотражения волн от границ слоя, пунктирной  - с учетом  4-х слагаемых поля в формуле (7). 

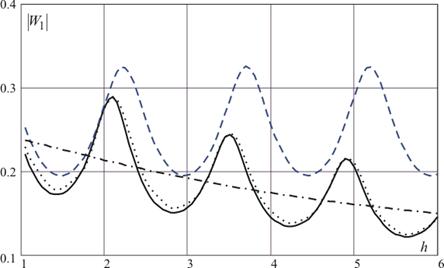
Рис. 2. - ,  

Литература:

1. Ляпин, А.А. Механико-математические модели в задачах активной сейсмологии [Текст]: Монография / Ляпин А.А., Селезнев М.Г., Собисевич Л.Е., Собисевич А.Л. – М.: ГНИЦ ПГК, 1999. 294 с.
2.  Углова, Е.В. Усталостная долговечность эксплуатируемых асфальтобетонных покрытий [Текст]: Монография /  Углова Е.В., Илиополов С.К., Селезнев М.Г. - Ростов-на-Дону: РГСУ. 2009. -244 c.
3.  Кадомцев М.И., Ляпин А.А., Тимофеев С.И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт» [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/719 (доступ свободный) – Загл. с экрана. – Яз. рус.   
4. Новацкий, В.   Теория упругости [Текст]: Монография / Новацкий В.   - М.: Мир, 1975. –872 с.
5. Уфлянд, Я.С.   Интегральные преобразования в задачах теории упругости [Текст]: Монография / Я.С. Уфлянд -Л., Наука. 1967. – 403 c.
6. Кадыров Р.Р., Ляпин А.А. Особенности возбуждения слоистых сред внутренними источниками колебаний  [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/981 (доступ свободный) – Загл. с экрана. – Яз. рус.   
7. Треногин, В.А.     Функциональный анализ [Текст]: Монография / В.А. Треногин–М.: Наука, 1980. –496 с.
8. Федорюк, М.В.  Асимптотика: интегралы и ряды [Текст]: Монография / М.В. Федорюк. - М.: Наука, 1987. – 544 с.
9. Pao Y., Gajewski R.R.     The generalized ray theory an transient responses of layered elastic solids // Phys. Acoust. Princ. And Meth. –1977. –13. –P.183-265.
10.  Romeo Maurizio    SH surface waves in layered half-spaces // Quart. J. Mech. And Appl. Math. –1997. –50, №4. –p. 581-595.