Нейросетевые модели в задачах исследования строительных конструкций
Аннотация
Дата поступления статьи: 28.11.2013Рассматривается обратная коэффициентная задача по определению свойств строительной конструкции с помощью аппарата нейронных сетей. В качестве модели взята нейронная сеть в виде полутораслойного предиктора с возможностью итерационного наращивания объема. Разработаны алгоритмы решения прямой и обратной задач многомерной аппроксимации.
Ключевые слова: Рассматривается обратная коэффициентная задача по определению свойств строительной конструкции с помощью аппарата нейронных сетей. В качестве модели взята нейронная сеть в виде полутораслойного предиктора с возможностью итерационного наращивания объе
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Актуальными являются обратные коэффициентные задачи по определению свойств строительной конструкции на основе экспериментальных данных [1,2]. Решение таких задач возможно с использованием аппарата нейронных сетей [3-9]. Нейросетевые модели целесообразно применять для начальной интерпретации диапазонов сигналов, а также для прогноза поведения конструкции при возможном изменении ее характеристик.
Пусть набор критериев ![]() определяет качественные свойства конструкции. Каждый из критериев
определяет качественные свойства конструкции. Каждый из критериев ![]() является функцией входных сигналов (параметров)
является функцией входных сигналов (параметров) ![]() , диапазоны изменения которых
, диапазоны изменения которых ![]() известны. По данным эксперимента найдены значения критериев
известны. По данным эксперимента найдены значения критериев ![]() на определенных наборах входных параметров. Число таких наборов (образцов) равно
на определенных наборах входных параметров. Число таких наборов (образцов) равно ![]() . Обозначим
. Обозначим ![]() - входы или значения
- входы или значения ![]() -го входного параметра для
-го входного параметра для ![]() -го образца;
-го образца; ![]() − выходы или значения
− выходы или значения ![]() -го критерия для
-го критерия для ![]() -го образца, найденные в результате эксперимента.
-го образца, найденные в результате эксперимента.
В качестве модели используется нейронная сеть в виде полутораслойного предиктора [10]. Сеть позволяет моделировать две задачи: задачу многомерной аппроксимации (прогноза) значений критериев и обратную задачу определения входных параметров по заданным значениям критериев.
Моделирование первой задачи заключается в том, что аппроксимируемые функции представляются в виде частичных сумм сходящегося ряда
![]() ,
, ![]() ,
,
где 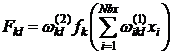 ,
, ![]() − составляющая ряда, соответствующая
− составляющая ряда, соответствующая ![]() -му потоку нейронов;
-му потоку нейронов;![]() −активационная функция;
−активационная функция; ![]() − коэффициенты синоптических связей первого и второго слоев потока нейронов. Схема сети для
− коэффициенты синоптических связей первого и второго слоев потока нейронов. Схема сети для ![]() -го потока показана на рис.1.
-го потока показана на рис.1.
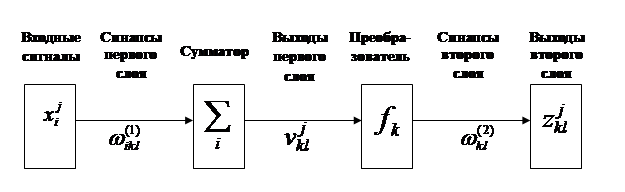
Рис.1. − Схема k-го потока сети
Особенностью сети такого типа является итерационное наращивание объема. Каждый последующий шаг, связанный с добавлением нового потока нейронов, осуществляется только после обучения предыдущего потока. При этом в качестве требуемых выходов добавленного потока нейронов рассматриваются ошибки аппроксимации предыдущего шага:
![]() ,
, ![]() ,
, 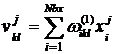 ,
, ![]() ,
,
где ![]() ,
,![]() - требуемые и найденные выходы для
- требуемые и найденные выходы для ![]() -го потока.
-го потока.
Коэффициенты ![]() синоптических связей рассчитываются с помощью процедуры обратного распространения из условия минимума функции оценки
синоптических связей рассчитываются с помощью процедуры обратного распространения из условия минимума функции оценки 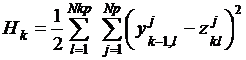 по итерационным формулам
по итерационным формулам ![]() ,
, ![]() ,
,
где ![]() - номер итерации. Поправки
- номер итерации. Поправки ![]() ,
,![]() выражаются через проекции
выражаются через проекции ![]() на оси
на оси ![]() ,
,![]() .
.
Шаг ![]() в процессе расчета корректируется для обеспечения монотонного убывания функции оценки. Если для очередного потока в результате корректировки весов достигается требуемый минимум функции оценки, то следующий поток нейронов не добавляется, и аппроксимируемая функция считается построенной.
в процессе расчета корректируется для обеспечения монотонного убывания функции оценки. Если для очередного потока в результате корректировки весов достигается требуемый минимум функции оценки, то следующий поток нейронов не добавляется, и аппроксимируемая функция считается построенной.
Алгоритм реализации задачи аппроксимации
- Инициализация: присвоение
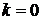 ; ввод значений
; ввод значений 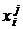 ,
,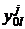 ,
,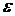 .
. - Добавление
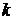 -го потока: присвоение
-го потока: присвоение 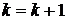 .
.
-
- Инициализация: присвоение
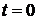 ; ввод значений
; ввод значений 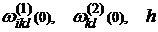 ,
, 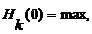
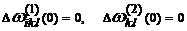 .
. - Итерация по
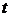 : присвоение
: присвоение 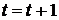 .
. - Корректировка коэффициентов
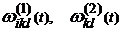 ; расчет
; расчет 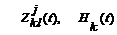 .
. - Проверка условия
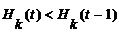 : если «true», то
: если «true», то 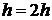 и переход на 2.e (проверка достижения заданной точности); если «false», то
и переход на 2.e (проверка достижения заданной точности); если «false», то 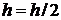 и переход на 2.c (пересчет итерации с измененным шагом).
и переход на 2.c (пересчет итерации с измененным шагом). - Проверка условия
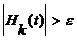 и
и 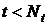 : если «true», то вычисление поправок
: если «true», то вычисление поправок 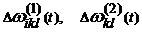 и переход на 2.b (нахождение следующей итерации для коэффициентов); если «false», то переход на 2.f (завершение программы или добавление нового потока).
и переход на 2.b (нахождение следующей итерации для коэффициентов); если «false», то переход на 2.f (завершение программы или добавление нового потока). - Проверка условия
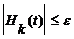 : если «true», переход на 3 (аппроксимация завершена); если «false», то переход на 2.g.
: если «true», переход на 3 (аппроксимация завершена); если «false», то переход на 2.g. - Проверка условия сходимости
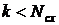 : если «true», то расчет
: если «true», то расчет 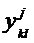 (требуемые выходы для следующего потока); запоминание
(требуемые выходы для следующего потока); запоминание 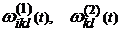 ; переход на 2 (добавление нового потока); если «false», то переход на 3 (аппроксимация не выполнена).
; переход на 2 (добавление нового потока); если «false», то переход на 3 (аппроксимация не выполнена).
- Инициализация: присвоение
- 3.Завершение программы.
Пусть в результате решения задачи аппроксимации найдено разложение ![]() ,
, ![]() для всех критериев, т.е. сеть обучена, и коэффициенты синоптических связей уже известны. В обратной задаче по известным значениям критериев
для всех критериев, т.е. сеть обучена, и коэффициенты синоптических связей уже известны. В обратной задаче по известным значениям критериев ![]() находятся соответствующие значения входных параметров
находятся соответствующие значения входных параметров ![]() . Отличие в решениях прямой и обратной задач состоит в том, что в задаче аппроксимации обучение сети осуществляется по коэффициентам синоптических связей, а в обратной задаче − по входным параметрам
. Отличие в решениях прямой и обратной задач состоит в том, что в задаче аппроксимации обучение сети осуществляется по коэффициентам синоптических связей, а в обратной задаче − по входным параметрам ![]() . На входы обученной сети подаются начальные значения
. На входы обученной сети подаются начальные значения ![]() из рассматриваемых диапазонов
из рассматриваемых диапазонов ![]() . Далее вычисляются значения выходов
. Далее вычисляются значения выходов ![]() по формулам
по формулам
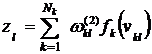 ,
, 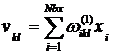 ,
, ![]() .
.
Последующие итерации ![]() ,
, ![]() рассчитываются с помощью процедуры обратного распространения из условия минимума функции оценки
рассчитываются с помощью процедуры обратного распространения из условия минимума функции оценки
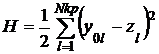 по итерационным формулам
по итерационным формулам ![]() ,
,
где ![]() - номер итерации. Поправки
- номер итерации. Поправки ![]() выражаются через проекцию
выражаются через проекцию ![]() на ось
на ось ![]() . Сходящийся итерационный процесс останавливается по условию достижения требуемого минимума функцией оценки
. Сходящийся итерационный процесс останавливается по условию достижения требуемого минимума функцией оценки ![]() .
.
Список литературы:
- Кадомцев М.И., Ляпин А.А., Шатилов Ю.Ю. Вибродиагностика строительных конструкций. [Электронный ресурс] // «Инженерный вестник Дона», 2012. - № 3. - Режим доступа: http://ivdon.ru/magazine/archive/ (доступ свободный) – Загл. с экрана. – Яз. рус.
- Кадомцев М.И., Ляпин А.А., Тимофеев С.И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт». [Электронный ресурс] // «Инженерный вестник Дона», 2012. - № 1. - Режим доступа: http://ivdon.ru/magazine/archive/ (доступ свободный) – Загл. с экрана. – Яз. рус.
- Абовский Н.П., Максимова О.М. Нейропрогнозирование результатов натурных испытаний строительных конструкций на основе эволюционной пошаговой модели с доучиванием. // Научная сессия МИФИ-2007. IХ Всеросс. науч.-техн. конф. «Нейроинформатика – 2007». Сборник научных трудов. В 3-х частях. Ч.1. М.: МИФИ, 2007 .− С.122-131.
- Максимова О.М. Разработка и применение нейросетевой технологии прогнозирования к задачам строительной механики и конструкций. //Труды Междунар. Конгресса «Наука и инновации в строительстве» SIB – 2008, Воронеж, 2008. − С.146-151.
- Абовский, Н. П Нейросетевые модели в задачах строительной механики / Н. П. Абовский, Т. В. Белобородова, О. М. Максимова, Л. Г. Смолянинова // Изв. вузов. Строительство, 2000. - № 7. – С. 6–14.
- Watkins, S., Akhavan, F., Dua, R., Chandrashekhara, K., and Wunsch. Impact-induced damage characterization of composite plates using neural networks. // Smart Materials and Structures, 2007, 16(2). – pp. 515-524.
- Park, J., Kim, J., Hong, D., Ho, D., and Yi. Sequential damage detection approaches for beams using time-modal features and artificial neural networks. // Journal of Sound and Vibration, 2009, 323(1-2). – pp. 451-474.
- Tsaregorodtsev V.G. Parallel implementation of back-propagation neural network software on SMP computers / Lecture Notes In Computer Science 3606 (PaCT-2005 Proceedings), Springer-Verlag, 2005. –pp.185-192.
- Нейронные сети и анализ данных. [Электронный ресурс]: http://neuropro.ru/links.shtml.
- Доррер М.Г. Аппроксимация многомерных функций полутораслойным предиктором с произвольными преобразователями. Методы нейроиформатики. //Сборник научных трудов. Под ред. А.Н. Горбаня, КГТУ, Красноярск, 1998. − С.130-151.