Многокритериальное принятие решений в условиях риска на основе интеграции мультиагентного, имитационного, эволюционного моделирования и численных методов

Аннотация

А.С. Антонова, К.А. Аксенов

Принятие управленческих решений в организационно-технических системах осложняется рисками появления в системах различных событий с заданной вероятностью.   В статье предложена методика поддержки принятия решений в условиях риска на основе интеграции  эволюционной, мультиагентной, имитационной моделей и численных методов. В ходе работы методики формируется множество альтернатив решений задачи, снимается многокритериальность оценок решений с помощью численного метода линейной свертки, снимается неопределенность поведения внешней среды с использованием  оптимизационного критерия Байеса-Лапласа. Разработанный метод применен к решению задачи планирования проектных работ; полученные результаты согласуются с решением задачи методом генетического алгоритма в условиях определенности.

Ключевые слова: риски принятия решений, мультиагентное моделирование, численные методы оптимизации решений, календарное планирование работ, эволюционное моделирование

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Процесс принятия решений в сложных организационно-технических системах (ОТС) представляет собой трудоемкую задачу, которую осложняют неполнота исходной информации, наличие множества показателей качества (критериев) оценки исходов альтернативных решений задачи, сокращение времени принятия решений и повышение требований к опыту и квалификации лиц, принимающих решения (ЛПР). Неполнота исходной информации связана с неопределенностью прогнозируемой ситуации, в рамках которой решение должно функционировать. И. Г. Черноруцкий в [1] выделяет два различных характера неопределенности: 1)  «природная» неопределенность, связанная с неопределенностью состояния внешней среды; 2) неопределенность типа «активный партнер», отражающая поведение других субъектов по выбору решения. Учет последней неопределенности приводит к постановке задачи принятия решений в условиях конфликта; анализом методов решения подобных задач занимается теория игр. В настоящей работе рассмотрим постановку задачи принятия решений в условиях неопределенности внешней среды и опишем метод принятии решений на основе интеграции мультиагентного, имитационного, эволюционного моделирования и численных методов.
Задача многокритериального принятия решений в условиях риска
Рассмотрим задачу многокритериальной оптимизации в условиях риска следующего вида:
, ,   (1)
где  – конечное множество альтернатив;
 – конечное множество состояний внешней среды;
 – функционал преобразования альтернативы x при состоянии z в некоторый исход;
 – конечное множество критериев оценки исходов альтернативы x;
 – конечное множество решений.
В общем случае множества X, Z, Y могут быть бесконечными. В случае конечных множеств значения {y_ij} задают матрицу решений. В задаче (1) каждый элемент матрицы решений представляет собой совокупность m оценок исходов альтернативы x при некотором состоянии среды z.
Согласно терминологии, предложенной И.Г. Черноруцким, при наличии знаний о вероятностях состояний среды принятие решений осуществляется в условиях риска; при отсутствии знаний – в условиях полной неопределенности.
Рассмотрим процесс приятия решений в условиях риска и определим множество вероятностей P пребывания внешней среды в состояниях Z: , .
В теории принятия решений существует ряд численных методов, предназначенных для снятия многокритериальности оценки исходов и неопределенности входной информации при решении задачи в условиях риска. Основную трудность при решении задачи (1) представляет определение функционала j, поскольку для реальных управленческих задач данный функционал должен учитывать накопленные статистические данные поведения системы, динамику протекающих в системе процессов и сценарную модель поведения ЛПР, что не всегда возможно представить аналитически. Применение мультиагентного, имитационного моделирования позволяет учесть предъявляемые к функционалу требования. Рассмотрим имитационную модель мультиагентных процессов преобразования ресурсов (МППР) [2] для формализации системных процессов и представления функционала j(x,z). Модель МППР интегрирует имитационное, ситуационное, экспертное, мультиагентное и концептуальное представления системы с целью проведения комплексного системного анализа.
Методика решения задачи на основе интеграции мультиагентного, имитационного, эволюционного моделирования и  численных методов
Рассмотрим методику решения задачи (1), включающую в себя следующие шаги.
Шаг 1. Описание множества критериев G оценки исходов.
Поскольку оптимизация решения задачи связана с поиском максимума значения (1), то критерии оценки исходов предполагается определять также с учетом максимизации оценки по отдельному критерию. При необходимости учета минимизирующего критерия следует заменить исходный критерий gi отношением  эталонного (начального) значения критериальной функции  к текущему значению критериальной функции gi:
, .   (2)
Шаг 2. Определение множества состояний внешней среды Z и вероятностей P пребывания внешней среды в состояниях Z.
Шаг 3. Определение функционала j с помощью модели МППР функционирования исследуемой системы в условиях влияния внешней среды.
Для разрабатываемой модели МППР входными параметрами будут являться значения альтернативы x и состояния среды z, а выходными параметрами – множество оценок исходов согласно выбранным критериям .
Шаг 4. Формирование множества альтернатив X.
При решении задач управления ОТС рассматривается область допустимых решений D, которая содержит множество оцениваемых альтернатив. Задача выбора конечного множества X из бесконечного множества D не является тривиальной, поскольку формируемое множество X должно включать удовлетворительное (эффективное, оптимальное) решение задачи в условиях определенности.  Рассмотрим применение эволюционного и имитационного, мультиагентного моделирования для формирования множества альтернатив X.
Пусть задана эволюционная модель (ЭМ) поиска лучшего решения задачи в условиях определенности (без учета вероятностных состояний внешней среды). Определим ЭМ с помощью простого генетического алгоритма (ГА) оптимизации решения поставленной задачи [3]. На вход ГА будем подавать набор случайных значений из множества D (особей начальной популяции в терминологии ГА), значения параметров ГА (количество итераций, вероятности применения генетических операторов), а на выходе –формировать  множество альтернатив X. Для расчета приспособленности особей (функции пригодности решений) применим модель МППР, входной информацией для которой служат значения управляемых параметров, закодированные в особи ГА, а на выходе формируется оценка особи с учетом динамических характеристик процессов системы [4].
Шаг 5. Формирование матрицы решений задачи многокритериальной оптимизации в условиях риска.
В результате применения к заданным альтернативам X функционала j  и оценки полученных исходов с помощью критериев G получим матрицу решений Y, представленную в таблице №1.
Таблица № 1
Матрица решений многокритериальной задачи в условиях риска

Шаг 6. Снятие многокритериальности задачи принятия решений.
Проведем замену векторного критерия оптимальности G на скалярный. Применим численный метод линейной свертки, подразумевающий выполнение линейного объединения всех частных критериев полезности  в один [1]:
; , , ,    (3)
где F(x, z) – функция реализации альтернативы x при состоянии среды z.
Весовые коэффициенты  рассматриваются как показатели важности отдельных критериев; они могут быть, как заданы ЛПР, так и вычислены, например, с помощью метода анализа иерархий Т.Л. Саати [5].
Применение метода линейной свертки предполагает наличие однородности оцениваемых критериев, которая может быть достигнута за счет использования при расчете критериев отношения (2).
Постановка задачи (1) с учетом (3) примет вид:
,.    (4)
Выражение (4) представляет собой классическую постановку однокритериальной задачи принятия решений в условиях риска. Матрица решений Y для данной задачи представлена в таблице №2.
Таблица № 2
Матрица решений задачи в условиях риска

Шаг 7. Снятие неопределенности задачи принятия решений и выбор альтернативы.
Пусть задана функция реализации (4), при этом F характеризует «доход», полученный от исхода, реализовавшегося при применении альтернативы x. Тогда согласно [1] задача (4) эквивалента задаче максимизации «среднего» дохода:
,    (5)
где черта сверху означаетматематическое ожидание величины;
J1(x) – функционал критерия математического ожидания (критерия Байеса-Лапласа).
Матрица решений задачи (5) приведена в таблице №3. Решением задачи (1) будет являться альтернатива:  [1].
Таблица № 3
Матрица решений задачи при применении критерия Байеса-Лапласа

…	…

Применение разработанной методики к решению задачи планирования проектных работ в условиях риска
Рассмотрим задачу календарного планирования проектных работ на предприятия ЗАО «Телесистемы» с учетом распределения трудовых ресурсов предприятия и привлечения ресурсов сторонних субподрядных организаций [6]. Задача заключается в нахождении такого календарного плана выполнения работ по портфелю проектов в течение года, при котором суммарные затраты на субподрядные работы минимальны, суммарный простой собственных отделов предприятия (проектного и производственного) минимален и коэффициент использования трудовых ресурсов предприятия максимален. Решение задачи осуществляется в условиях риска появления 4-х дополнительных комплексных проектов (требующих наличия свободных ресурсов как проектного, так и производственного отделов предприятия) весной, летом, осенью и зимой.
Применим разработанную методику многокритериального принятия решений в условиях риска к рассматриваемой задаче календарного планирования.
Шаг 1. Опишем следующие критерии оценки полезности исходов: суммарную стоимость субподрядных работ по портфелю проектов SS, общий простой проектного SUp и производственного SUm отделов за год в процентах, коэффициент использования трудовых ресурсов предприятия My.
Методика расчета первых трех критериев описана в [4], их применение предполагает минимизацию оценок исходов. Последний критерий, My, предназначен для оценки степени равномерного использования ресурсов за период T. Формула расчета коэффициента использования трудовых ресурсов представлена ниже [7]:
,    (6)
где i –день поступления запроса на свободные ресурсы для выполнения операций;
k – день первичного формирования запроса на ресурсы;
ResourceDemandi – требуемый объем ресурсов для выполнения операций в день i.
Шаг 2. Определим множества Z и P через множество возникающих в системе событий  и множество вероятностей возникновения событий . Рассмотрим множество L, состоящее из следующих r=8 событий: появление/непоявление дополнительного комплексного проекта в каждое из времен года. Граф определения состояний системы с помощью событий представлен на рис. 1.

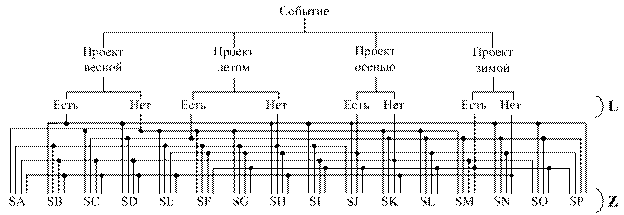
Рис. 1. – Граф состояний системы
В результате построения графа состояний системы выделено s=16 состояний z_i {SA,...,SP}, причем каждое состояние характеризуется одновременным выполнением h событий множества L: , , , , . Определим вероятность pi пребывания системы в состоянии z_i согласно выражению:
, , , . (7)
Для решаемой задачи r=8, h=4, s=16, т.е. рассматривается 8 событий, по которым определяется 16 состояний системы, причем каждое состояние задается одновременным выполнением 4 событий. Вероятности наступления событий заданы в таблице №4.

Таблица № 4
Множества событий L и вероятностей наступления событий PL

Вероятности нахождения системы p_i в одном из состояний z_i, рассчитанные при данных начальных условиях, представлены в таблице №5.
Таблица № 5
Множества состояний среды Z и вероятностей пребывания системы в этих состояниях P

Рассчитаем для примера вероятность нахождения системы в состоянии z₁=SA:   (см. рис. 1). Воспользуемся формулой (7):
.
Шаг 3. Решение поставленной задачи планирования работ предполагает разработку модели МППР, описывающей процесс исполнения работ по портфелю проектов. За основу разрабатываемой модели исполнения работ была взята модель МППР решения задачи календарного планирования, построенная в системе динамического моделирования ситуаций BPsim.MAS и описанная в [6]. Данная модель была дополнена следующими входными параметрами: признаками нахождения системы в одном из анализируемых состояний (да/нет) для интеграции модели с численными методами оптимизации решения. Также модель была расширена расчетом дополнительной выходной характеристики – коэффициента использования трудовых ресурсов предприятия согласно (6).
Шаг 4. Сформируем множество альтернатив X с помощью интеграции имитационного, мультиагентного и эволюционного моделирования. Задачу интеграции предложенных методов моделирования решает интеллектуальный агент (ИА) генетической оптимизации, разработанный в среде BPsim.MSN на основе технологии проектирования визардов [4]. В работе [4] ИА был применен к решению задачи планирования проектных работ в условиях определенности. В ходе работы ГА было получено 10 поколений особей, хранящих в своих генах информацию о календарных сроках начал операций по проектам портфеля. Выберем в качестве множества альтернатив Х набор раскодированных особей 7-го поколения работы ГА, в котором было найдено наилучшее решение задачи согласно проведенным исследованиям [4]. Зададим размерность множества альтернатив n=8.
Шаг 5. Сформируем матрицу решений поставленной задачи многокритериальной оптимизации в условиях риска путем оценки выбранных альтернатив  с помощью набора критериев  для каждого состояния системы z_i. Для этого проведем серию из  экспериментов с разработанной моделью МППР, на вход которой будем подавать анализируемую альтернативу x_i и признаки наступления/ненаступления событий множества L для формирования анализируемого состояния z_j, а на выходе будем наблюдать значения описанных критериев для текущих  и , , . Результаты экспериментов сохраним в таблицу №1.
Шаг 6. Проведем снятие многокритериальности решаемой задачи путем применения метода линейной свертки (3), предварительно приведя рассматриваемые критерии к однородному виду с помощью (2). В результате выполнения описанных процедур свертка критериев в функцию реализации примет следующий вид:
,    (8)
где надстрочный индекс Init означает критериальную оценку эталонного экспертного решения задачи планирования.
Шаг 7. Проведем снятие неопределенности поставленной задачи с применением численных методов. Рассмотрим матрицу решений, сформированную на шаге 6. Зададим начальные значения коэффициентов формулы (8): a₁=0.5; a₂=0.2; a₃=0.2; a₄=0.1.
Воспользуемся критерием Байеса-Лапласа (5) для сведения матрицы решений к вектору решений . После выполнения преобразований имеем J₁(x)={104.0; 95.8; 90.4; 121.5; 120.7; 127.7; 143; 126.5}. Нетрудно определить, что наилучшим решением является альтернатива x₇ со значением J₁(x₇)=143.
Исследуем устойчивость найденного решения x₇при применении критерия Байеса-Лапласа для снятия неопределенности. Для этого проведем серию экспериментов по нахождению векторной функции оценки альтернатив при разных начальных условиях. Будем изменять степень важности отдельных критериев при формировании функции реализации, т.е. коэффициенты α_i формулы (8), и  вероятности наступления событий pL (таблица №4). План проведения экспериментов представлен в таблице №6.
Таблица № 6
План экспериментов по исследованию устойчивости найденного решения задачи

            По результатам проведенных экспериментов была построена зависимость векторной функции Байеса-Лапласа, компонентами которой являются оцениваемые альтернативы, от изменения начальных условий (рис. 2).

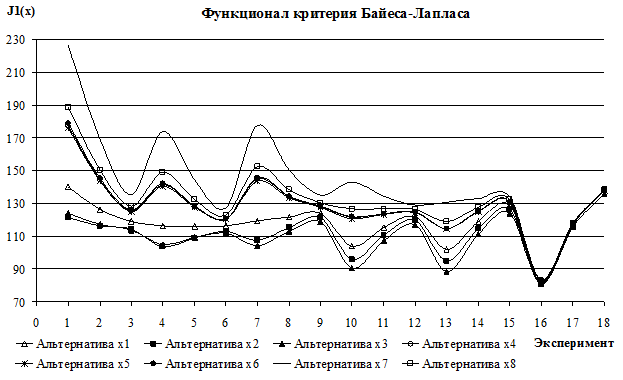
Рис. 2. – Исследование устойчивости решений при применении критерия Байеса-Лапласа

Анализ поведения функционала J₁(x) при различных начальных условиях показал, что доминирующее значение альтернативы x₇ сохраняется при всех анализируемых ситуациях. При этом превосходство x₇ максимально в случае равновероятностных  событий появления 4-х дополнительных проектов (с вероятностями, не превышающими 0.75) и выборе в качестве наиболее важного критерия минимизацию суммарной стоимости субподрядных работ. Превосходство решения x₇ минимально (правая часть графика) в случае  высоких вероятностей появления 4-х дополнительных проектов и предпочтении любого из критериев. Таким образом, в результате применения критерия Байеса-Лапласа, можно сделать вывод о принятии решения в пользу альтернативы x₇, обладающей устойчивостью к изменениям начальных условий задачи (факторов риска). Полученные данные согласуются с результатами работы [4].
В результате исследования применимости численных методов оптимизации к решению задач управления ОТС был сделан вывод о целесообразности интеграции численных методов и мультиагентного, имитационного, эволюционного моделирования. Совместное применение предложенных подходов обеспечивает учет накопленной статистики поведения системы, динамику протекающих системных процессов и сценарную модель поведения ЛПР в ходе проведения оценки исходов анализируемых альтернатив. Кроме того, использование имитационного и эволюционного моделирования позволяет формировать множество альтернатив, включающее в себя  удовлетворительное (эффективное, оптимальное) решение задачи в условиях определенности с целью дальнейшей оценки решения в условиях неопределенности.
Таким образом, интеграция предложенных подходов моделирования и численных методов обеспечивает проведение полнофакторного анализа рассматриваемых рисков возникновения (нежелательных) событий в системе и поддержку обоснованного принятия решений в условиях риска.
Работа поддержана грантом РФФИ № 12-07-31045.

Литература

1. Черноруцкий И.Г. Методы принятия решений [Текст] / И.Г. Черноруцкий.– СПб.: БХВ-Петербург, 2005. – 416 с.
2. Аксенов К.А. Динамическое моделирование мультиагентных процессов преобразования ресурсов [Текст] / К.А. Аксенов, Н.В. Гончарова.– Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006.–311 с.
3. Бионические информационные системы и их практические применения [Текст] / Под ред. Л.А. Зинченко, В.М. Курейчика, В.Г. Редько. – М.: ФИЗМАТЛИТ, 2011. – 288 с.
4. Антонова А.С., Аксенов К.А. Генетическая оптимизация при решении задачи планирования проектных работ [Электронный ресурс] // Современные проблемы науки и образования. – 2012, № 6. – Режим доступа: http://www.science-education.ru/106-7409 (доступ свободный) – Загл. с экрана. – Яз. рус.
5. Саати Томас Л. Принятие решений при зависимостях и обратных связях: Аналитические сети [Текст] Пер. с англ. / Науч. Ред. А.В. Андрейчиков, О.Н. Андрейчикова. – М.: Издательство ЛКИ, 2008. – 360 с.
6. Аксенов К.А., Антонова А.С. Применение имитационного моделирования и технологии интеллектуальных агентов для решения задачи управления проектами [Текст] // Научно-технические ведомости СПбГПУ № 4(128) 2011. Информатика. Телекоммуникации. Управление. г.С.-Петербург С.27-36.
7. Sriprasert, E., Dawood, N. N. Genetic algorithms for multi-constrained scheduling: an application for the construction industry [Текст] // Proceedings of the CIB W78's 20th International Conference on Construction IT, Construction IT Bridging the Distance, CIB Report 284, Waiheke Island, New Zealand, 23-25 April 2003. P. 341-353.