Моделирование листостебельных материалов с помощью теории графов
Аннотация
Статья посвящена моделированию растительных объектов, а именно, листостебельных материалов. Рассмотрены растительные объекты с различными типами ветвления с учетом их развития. Построены математические модели с помощью теории графов.
Ключевые слова: модель, растительный объект, стебель, ориентированный граф
В настоящее время уделяется большое внимание вопросам математического моделирования растительных объектов. Растительные материалы представляют собой объекты сложной геометрической формы и построение моделей этих объектов очень трудный процесс. Рассмотрим построение моделей обобщенных листостебельных структур с помощью теории графов с использованием ориентированных графов с непустым множеством источников и непустым множеством стоков. Необходимо выбрать обобщенную аналитическую модель для описания архитектоники данного растительного объекта. Листостебельные растения представляют собой растительные объекты с различной скелетной структурой. На рис. 1 представлены обобщенные модели с различными типами ветвления.
а).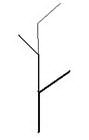 б).
б).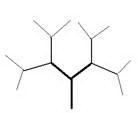 в).
в). г).
г).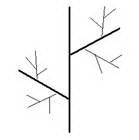
Рис. 1. Модели листостебельных структур в виде графов с различными типами ветвления (а–симподиальное,б–дихотомическое, в,г – моноподиальное симметричное,несимметричное)
Для описания этих моделей используются сети. Данный объект можно представить в матричной форме, при этом строятся матрицы ребер и узлов. Проанализировав структуру этих матриц можно отметить, что они являются почто квазидиагональными матрицами. В недиагональных блоках матрицы ребер все элементы равны нулю, а блоки имеют похожую структуру, что нельзя сказать о структуре матрицы узлов (рис. 2).
Для моноподиального несимметричного и дихотомического типов ветвления в области нулевых матриц встречаются ненулевые вектора и ненулевые матицы размером 4x2 и 2x4. Характерные особенности в матрице ребер: для каждого типа ветвления в состав матрицы входят ненулевые матрицы с характерным расположением элементов:
а).для симподиального типа ветвления матрица
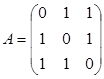 ;
;
б).для дихотомического типа ветвления матрица по диагонали
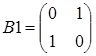 ;
;
и в области нулевых элементов симметрично диагонали расположены матрицы

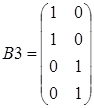 ;
;
в). моноподиального симметричного типа ветвления матрица
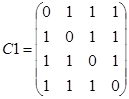 ;
;
г). моноподиального несимметричного типа ветвления матрица
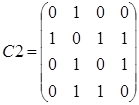
а).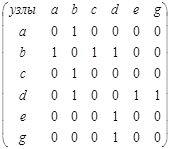 б).
б).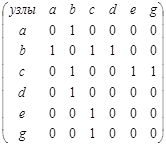 в).
в).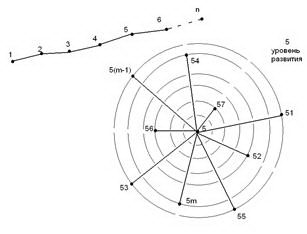 г).
г).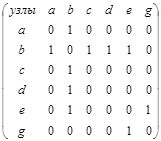
Рис. 2 . Матрицы узлов для листостебельных структур в виде графов с различными типами ветвления ( а – симподиальное, б – дихотомическое, в,г – моноподиальное симметричное, несимметричное)

Рис. 3. Модель развития листостебельного растения (1 – начало роста; 2 – росток; 3 – появление первых листочков; 4 – дальнейшее развитие листочков; 5– развитие ветвей;6 – дальнейшее развитие ветвей; …..; n – происходит увядание растения)
Рассмотренные модели листостебельных материалов позволяют создать математические модели технологического процесса в виде графа и идентификации растительных объектов.
Радиальное изображение графа используется для описания математической модели развития растительного объекта. В качестве вершины размещаемой в центре берется один из уровней развития растения (рис.3). Из вершины выходят ребра, которые характеризуют направления ветвей. Рассмотрим 5 уровень развития растительного объекта.
Вершина 5 является начальной вершиной ребра, а каждая из точек 5i ( i=1,…,n) будет конечной вершиной ребра. Расстояние между вершинами 5 и 5i будет длиной ребра и является самым коротким путем между этими вершинами. Диаметром графа будет наибольшее расстояние между вершинами 5 и наиболее удаленной вершиной.
На уровнях 5,6,.. растительный объект имеет наибольшую массу и ветви имеют максимальные значения длины. Если найти диаметр графа, то можно построить окружности с радиусами, кратными числам, которые характеризуют массу растения. Если длина i-го ребра попадает в границы построенных окружностей и большее количество ребер определяет зону с наибольшей растительной массой.
Для компьютерной реализации обобщенной математической модели развития растительного объекта лучше использовать модель в виде ориентированного дерева.
Рассмотрим модель в виде ориентированного дерева. Развитие растения идет от вершины 1 к вершине m и a, b, c, d, e, f, h … являются ребрами. На каждом этапе развития происходит разветвление на n направлений с вершинами j1,…,j n, где j=1,…,m. Из каждой j вершины выходят ребра с различной длиной ai, bi, ci, di, ei, fi, hi, где i=1,…, n. Модель можно представить в матричной форме согласно числу уровней и направлений. Ребра представлены буквами и числами. Буква соответствует уровню развития, цифра – направлению развития. Узлы представлены цифрами соответствующим образом. Так как учитываем направление роста растения, то матрицы узлов и ребер будут следующего вида:
 и
и  ,
,
где матрицы Aj , Bj и О равны:
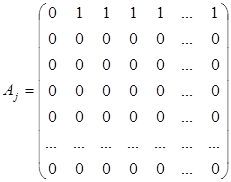
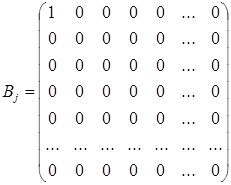
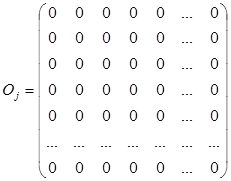
В матрице ребер и узлов использованы следующие обозначения. Например, узел i (i=1,…,m) связан с узлами j1,…,jn, то ставим 1, если нет – то 0. В матрице ребер 1 означает, что ребра отходят от линии уровней, в противном случае – нет. Для каждого ребра задаем его длину, которая характеризует верви растения. Если длина векторов a, b, c, d, e, f, h в линии уровней увеличивается, то происходит рост растительного объекта..
Возможности теории графов позволяют построить модели растений со сложной геометрией. Они позволяют более гибко размещать элементы скелетной структуры растений и обходиться без пересечения. Долгое время в различных технологических процессах переработки сельскохозяйственной продукции для описания растительных объектов использовались упрощенные модели, без учета реальной формы. Для повышения эффективности данных процессов необходимо совершенствование рабочих органов, введение новых конструктивных решений и использование компьютерной техники. Именно такие перспективы открывает математическое моделирование растительных материалов.
Дальнейшее развитие целесообразно вести в следующих направлениях: разработка конкретных технологических процессов. создание программного обеспечения моделирования сложных процессов, в которых участвуют растительные объекты.
Литература
-
Мандельброт Б. Фрактальная геометрия природы. – М.: Мир, 1982.
-
Раздорский В.Ф. Архитектоника растений. – М.: Советская наука, 1955.
-
Математическое моделирование./ Дж. Эндрюс, Р. Мак – Лоун. – М.: Мир, 1979.
-
Владимирский Б.М., Горстко А. Б., Ерусалимский Я. М. Математика. Общий курс. – СПб.: Лань, 2002.