Аномалии астрономической рефракции и их учет

Н.Н. Редичкин; И.Н. Редичкин

Аномалии астрономической рефракции и их учет

Аннотация

Н.Н. Редичкин, И.Н. Редичкин

При выполнении измерений зенитных расстояний небесных светил необходимо учитывать не только углы астрономической рефракции, но и ее аномалии. Предложен метод учета аномалий рефракции по результатам наблюдений небесных светил вблизи горизонта.

Ключевые слова: Астрономическая рефракция, Зенитное расстояние, Атмосфера, Аномалии рефракции, Азимут

25.00.32 - Геодезия

Исследования, выполненные в работах [1], [2], [3] позволяют считать, что при измерении зенитных расстояний ( ζ ) небесных светил необходимо учитывать не только углы астрономической рефракции (r_а), на и аномалии рефракции (Δr_а), которые определяют по формуле:

(Δr_а) = r_а^т - r_а^изм (1)

где: r_а^т – теоретическая рефракция (вычисленная по формулам или таблицам); r_а^изм - измеренная рефракция.

Углы (Δr_а) возникают из-за того, что принятая для вывода формул рефракции сферическая модель атмосферы, нарушается. Образуются наклоны изодиоптрических поверхностей. Нормаль к ним не совпадает с отвесной линией, образуя некоторый угол i равный дуге Zn (рис.1). В этом случае рефракция происходит не в вертикальной плоскости, а в плоскости, содержащей нормаль, луч падающий и луч преломленный. Такая рефракция называется аномальной. Аномальная рефракция изменяет не только зенитные расстояния, но и азимуты (А) светил.

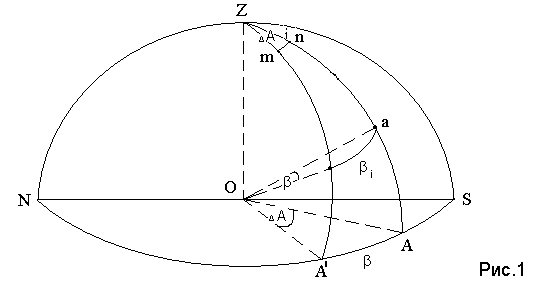
На зенитных расстояниях ζ < 70⁰ аномалии рефракции сравнимы с ошибками измерений. Для их учета на этих ζ можно использовать значения Δr_а, полученные по результатам наблюдений небесных светил вблизи горизонта, где r_а могут достигать величин от нескольких секунд до нескольких минут, а иногда и градусов [1]. Для определения i – общего наклона изодиоптрических слоев атмосферы в данном направлении, в работе [4] предложено использовать результаты измерений зенитных расстояний и азимутов небесных светил вблизи горизонта. Получена формула:

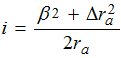(2)

В формуле (2) Δr_а находились по (1); β = ΔА = А - А^/ , где А^/ -измеренный азимут светила; А- азимут светила, вычисленный без учета наклонов изодиоптрических поверхностей по формуле, полученной из соотношений параллактического треугольника с известными значениями склонения (δ), широты (φ) и часового угла (t), тогда :

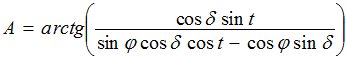(3)

Используя результаты наблюдений небесных светил вблизи горизонта по (1), (2), (3) вычисляют i и Δr_а. Для того, чтобы в этом направлении определить аномалии на ζ<70⁰ из формулы (2) найдем:

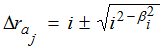(4)

где β_i - дуга пространственного угла а0в (рис.1), определяемая из сферического треугольника Zав по формуле:

cosβ_i = cos(Zа ) cos (Zв ) + sin(Za)sin(Zв) cosΔА (5)

Полагая в (5) Zа = Zв = ς получим:

β_i = arc cos (cos²ζ + sin²ζ cosΔA) (6)

Для расчетов по (4) воспользуемся данными, приведенными в [4] (табл.1). Углы ΔA, Δr_аи i получены по результатам измерений ζ и А^/ звезды αVir (Cпика) вблизи горизонта.

Таблица 1

Результаты вычислений аномалий рефракции

№ пп	ζ	r_а^т	r_а^изм	А^/	ΔА	Δr_а	i
1	86⁰44^/39,2^//	609,9^//	612,4^//	71⁰28^/45,2^//	-7,0^//	-2,5	-11,1
2	87⁰13^/50,8^//	689,9^//	695,6^//	72⁰00^/01,45^//	-10,3^//	-5,7	-12,2
3	87⁰37^/13,6^//	757,2^//	766,4^//	72⁰24^/59,0^//	-11,2^//	-9,2	-11,4
4	88⁰07^/07,6^//	850,9^//	857,5^//	72⁰56^/51,6^//	-7,3^//	-6,6	-7,3
5	88⁰27^/01,2^//	953,4^//	981,9^//	73⁰18^/38,2^//	-12,3^//	-28,5	-16,9
					ΔА_СР=-9,6		I_СР= -11,8^//

В таблице величины r_а^тполучены методом численного интегрирования [5]; величины r_а^изм = Z – ζ, где Z= arc cos (sinφ sinδ +соsφ cosδ cost); величины i получены по формуле (2) с учетом того, что β = ΔА_ср (табл.1).

На основании данных, приведенных в табл.1, выполнены расчеты значений Δr_а по (4) в зависимости от величины ζ. Получены результаты, приведенные в табл.2.

Таблица 2

Вычисление аномалий рефракции для различных зенитных расстояний звезд

	20	25	30	35	40	45	50	55	60	65	70
Δr_а	0,46″	0,71″	1,12″	1,35″	1,74″	2,14″	2,57″	2,99″	3,42″	3,82″	4,18″

В табл. 2 для расчетов по (4) принято, что i=i^cp (табл.1), а величина βⁱ по формуле (6).

Из табл. 2 видно, что предложенный способ учета аномалий рефракции может значительно улучшить результаты наблюдений при измерении зенитных расстояний небесных светил на ζ<70°.

Литература

1. Колчинский И.Г. Рефракция света в земной атмосфере (Обзор). - Киев.: Наукова думка, 1967.-44с.

2. Киричук В.В. Геодезическая рефракция и аномалия астрономической рефракции на больших зенитных расстояниях (Z=88,89,90°). - В сб.: Геодезия, картография и аэрофотосъемка. - Львов. Межвед.респ.научно-техн. сборник, вып. 13, 1971, с.36-43.

3. Нефедьева А.И. Аномалии рефракции. - В сб.: Современные проблемы позиционной астрометрии. М.: МГУ, 1975, с.110.

4. Редичкин И.Н. Определение наклонов изодиоптрических поверхностей по результатам измерений зенитных расстояний и азимутов опорных звезд. - В сб.: Прикладная геодезия, Из-во РГСУ, г.Ростов-на-Дону, 2001, с. 7-22.

5. Редичкин И.Н. Вычисление углов астрономической рефракции вблизи горизонта различными способами и сравнение результатов. - В сб.: Прикладная геодезия, Из-во РГСУ, г.Ростов-на-Дону, 1999, с. 93-102.