Криозондовый магнитометр
Аннотация
Рассмотрена задача взаимодействия взаимно перпендикулярных магнитных полей в сверхпроводниках. Показана возможность использования нелинейной восприимчивости сверхпроводников для измерения магнитного поля, проведена оценка чувствительности криозондового магнитометра.
Ключевые слова: сверхпроводник, магнитометр, СКВИД, криотрон, скрещенные магнитные поля, нелинейный магнетик, криозонд
При выборе магнитно-чувствительных элементов (далее МЧ-элементов) для измерения магнитных полей одним из главных принципов является обеспечение относительно высокой чувствительности при одновременно невысокой сложности установки. Вместе с тем должен обеспечиваться широкий комплекс требований к диапазону измерений и частотному диапазону, поэтому выбор типа МЧ-элемента будет зависеть от области и условий применения. Достоинства и недостатки того или иного метода измерения магнитного поля обуславливаются физическими эффектами, лежащими в основе.
Возможности датчиков Холла ограничены по ряду причин. Это обусловлено, прежде всего, низкой приведенной чувствительностью (0,1 ÷ 1 В/Тл), и сильной зависимостью параметров датчика от температуры. Поскольку остаточное напряжение датчика Холла принципиально нельзя получить меньше 0,1 ÷4 мВ, порог чувствительности при абсолютном измерении магнитных полей составляет 0,1 мТл. В полупроводниковых магниторезисторах обычно используются материалы с высокой подвижностью носителей заряда. Зависимость сопротивления такого резистора от индукции линейна только при значениях индукции, превышающих 0,3÷0,5 Тл. Для меньших значений индукции зависимость сопротивления близка к квадратичной, при этом изменение сопротивления магниторезистора, характеризующее магниточувствительность, резко снижается и составляет примерно 0,1 %/Тл. Температурный коэффициент полупроводниковых магниторезисторов составляет 1¸3 %/К. Относительно высокая чувствительность (1 ¸ 5 В/Тл) и термостабильность магнитодиода реализуется только в сочетании с подмагничивающим полем. Необходимо отметить также, что нелинейность, разброс характеристик и влияние температуры на коэффициент преобразования магнитодиода проявляются неодинаково в разных магнитных полях. Экспериментальные зависимости спектральной плотности шума магнитотранзисторов различных типов проводимости показывают, что для них пороговая чувствительность на частотах выше 1 кГц равна 0,005÷ 2 мкТл. Однако магнитотранзисторы имеют высокий уровень фликкер шумов, более 3 мкТл, и поэтому не могут применятся для измерений слабых постоянных или медленно меняющихся магнитных полей. Минимальное значение измеряемого магнитного поля магниторезистивными тонкопленочными преобразователями, соответствующее уровню собственных шумов, составляет примерно 0,1 мкТл. То есть чувствительность тонкопленочного магниторезистора такая же как у Холловского магнитометра.
Наиболее высокой чувствительностью обладают магнитометры, использующие нелинейные свойства некоторых материалов. Исследования, посвященные изучению взаимодействию взаимно перпендикулярных магнитных
полей в нелинейных магнетиках имеют почтенный возраст [1]. Как правило, в качестве такой нелинейной среды рассматривают ферромагнитные материалы и среды. Одним из практических результатов таких исследований стала разработка феррозондовых магнитометров, обладающих рекордной (для не квантовых измерителей) чувствительностью. Вместе с тем, хотя современная теория ферромагнетизма не позволяет аналитически описывать гистерезис, анализ работы феррозонда показывает, что гистерезисные потери являются фундаментальным ограничением порога чувствительности феррозондовых магнитометров [2].
Сверхпроводящие материалы также обладают нелинейными магнитными свойствами. Поскольку потери в сверхпроводниках в радиочастотном диапазоне пренебрежимо малы, это позволяет использовать нелинейную восприимчивость сверхпроводников для измерения слабых магнитных полей [3]. Можно ожидать, что взаимодействие взаимно перпендикулярных магнитных полей в сверхпроводниках позволит разработать магнитометры, не уступающие по чувствительности квантовым, например, сквидам [4].
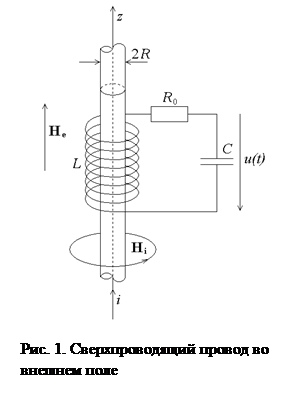
Пусть чувствительным элементом сверхпроводникового магнитометра, который можно назвать криозондовым, является тонкая проволока из сверхпроводника второго рода диаметром 2R, причем ξ << R << λ, где ξ – длина когерентности, а λ– глубина проникновения. Запишем для проволоки, находящейся во внешнем продольном однородном магнитном поле He, по которой течет ток i (рис. 1), уравнения Гинзбурга-Ландау [5]:
![]() , (1)
, (1)
![]() (2)
(2)
![]() , (3)
, (3)
где n - вектор нормали к поверхности сверхпроводника, ![]() – нормированный параметр порядка, A(r) – векторный потенциал магнитного поля, F0 ≈ 2,07×10-15 Вб – квант магнитного потока.
– нормированный параметр порядка, A(r) – векторный потенциал магнитного поля, F0 ≈ 2,07×10-15 Вб – квант магнитного потока.
Выберем цилиндрическую систему координат так, чтобы ось z совпадала с осью проволоки. Пусть напряженность внешнего магнитного поля равна He = He(r)ez = const. Магнитное поле, создаваемое током, имеет вид Hi = Hi(r)eφ= const![]() . Выберем калибровку вектор потенциала A
. Выберем калибровку вектор потенциала A![]() таким образом, чтобы функция Y была вещественной. Тогда уравнения (1) - (3) сводятся к нелинейным дифференциальным уравнениям (4) - (6) с действительными коэффициентами и граничным условиям (7) к ним:
таким образом, чтобы функция Y была вещественной. Тогда уравнения (1) - (3) сводятся к нелинейным дифференциальным уравнениям (4) - (6) с действительными коэффициентами и граничным условиям (7) к ним:
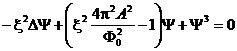 (4)
(4)
![]() , (5)
, (5)
![]() , (6)
, (6)
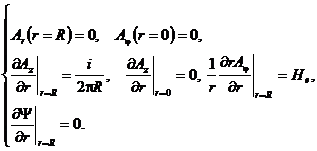 (7)
(7)
В силу симметрии задачи можно считать, что параметр порядка Y и вектор потенциал A зависят только от координаты r. Тогда из уравнения (6) следует Ar(r) º 0, что согласуется с первым граничным условием (7) Таким образом, вектор A имеет только z и φ компоненты: A = Az(r)ez+Aφ(r)eφ. Введем безразмерную координату ![]() и безразмерные компоненты вектор-потенциала
и безразмерные компоненты вектор-потенциала ![]() ,
, ![]() где
где ![]() , и обозначим
, и обозначим ![]() ,
, ![]() – малые параметры. Тогда уравнения (4), (5) и (7) принимают вид
– малые параметры. Тогда уравнения (4), (5) и (7) принимают вид
![]() , (8)
, (8)
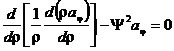 , (9)
, (9)
![]() (10)
(10)
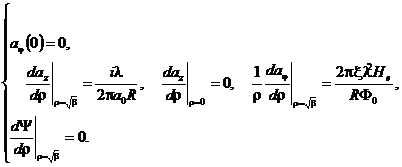 (11)
(11)
Если потребовать дополнительно, чтобы при ![]() выполнялись условия:
выполнялись условия:
![]() , (12)
, (12)
то уравнения (8) – (10) можно решать методом последовательных приближений, положив Ψ = Ψ0 + aΨ1 + bΨ2 + … . Подставляя это разложение в уравнение (8) и приравнивая коэффициенты при соответствующих степенях a и b, получим Ψ0 = 1, Ψ1 = 0, ![]() . Тогда уравнения (9) – (12) принимают вид:
. Тогда уравнения (9) – (12) принимают вид:
![]() , (13)
, (13)
![]() , (14)
, (14)
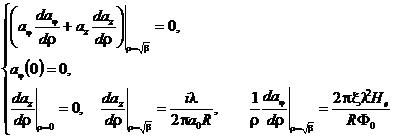 , (15)
, (15)
![]() . (16)
. (16)
Найдем приближенное решение уравнений (13) и (14), используя метод регулярного разложения по малому параметру β, в виде:
az(Ρ) = az0(Ρ) + βaz1(Ρ) + β2az1(Ρ) + …,
aφ(Ρ) = aφ0(Ρ) + βaφ1(Ρ) + β2aφ1(Ρ) + …,
С учетом граничных условий (15) в нулевом приближении, приравнивая коэффициенты при соответствующих степенях, получим:
![]() ,
,
где I0(Ρ) и I1(Ρ) – модифицированные функции Бесселя первого рода нулевого и первого порядков, соответственно.
Используя известное фундаментальное решение уравнения (13), следующее приближение решения уравнения имеет вид:
![]()
где ![]() - детерминант Вронского, K1(Ρ)– модифицированная функция Бесселя второго рода первого порядка. Тогда приближенное решение второго уравнения системы (8) может быть записано следующим образом:
- детерминант Вронского, K1(Ρ)– модифицированная функция Бесселя второго рода первого порядка. Тогда приближенное решение второго уравнения системы (8) может быть записано следующим образом:
![]()
Оценим величину магнитного потока через поперечное сечение сверхпроводящей проволоки. Приближенно вычисляя интегралы, входящее в последнее выражение, раскладывая модифицированные функции Бесселя вблизи нуля (Ρ << 1) и ограничиваясь линейными по r слагаемыми, получим:
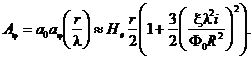
Откуда:
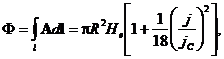 (17)
(17)
где ![]() - критическая плотность тока [5], j = i/S, S = ΠR2 – площадь поперечного сечения зонда.
- критическая плотность тока [5], j = i/S, S = ΠR2 – площадь поперечного сечения зонда.
Оценим порог чувствительности криозондового магнитометра. Пусть по зонду протекает переменный ток i(t) = i0sin(ϖ0t), создающий в нем плотность тока j(t) = j0sin(ϖ0t), близкую к критической. Положим j0 = i0/S = 0,9jC. Как и в феррозондовом магнитометре, сверхпроводящая проволока является сердечником LC контура с резонансной частотой близкой к 2ϖ0 (рис. 1). Если катушка индуктивности является длинным соленоидом, содержащим n витков, то:
![]() , (18)
, (18)
где H0![]() постоянное или медленно меняющееся измеряемое магнитное поле, q(t) – заряд на конденсаторе C.
постоянное или медленно меняющееся измеряемое магнитное поле, q(t) – заряд на конденсаторе C.
Колебания в резонансном контуре описываются уравнением:
![]() . (19)
. (19)
Подставляя в уравнение (19) выражение (17) для магнитного потока через сверхпроводящий зонд с учетом соотношения (18), получим дифференциальное уравнение второго порядка:
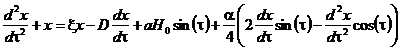 , (20)
, (20)
где обозначено ![]() , τ = 2ϖ0t, δ= R0/2L(1+a), q = q0x, a = Sna2/(2Lϖ0q0), D = δ/ϖ0,
, τ = 2ϖ0t, δ= R0/2L(1+a), q = q0x, a = Sna2/(2Lϖ0q0), D = δ/ϖ0, ![]() , a = (j0/6jC)2.
, a = (j0/6jC)2.
Поскольку a << 1, найдем решение уравнения (20) методом последовательных приближений в виде x = x0 + ax1 + … . В нулевом приближении, система описывается уравнением:
![]() .
.
Решение имеет вид:
![]() .
.
При точной настройке контура (ξ << D) для выходного напряжения преобразователя получаем:
![]() , (21)
, (21)
где Q = 1/D – добротность контура.
Из формулы (21) видно, что напряжение на контуре u(t) осциллирует с частотой 2ϖ0 синхронно с переменным током i(t), текущим по проволоке, что позволяет использовать метод синхронного детектирования. Амплитуда U0 выходного напряжения пропорциональна потоку F измеряемого магнитного поля H0 через поперечное сечение сверхпроводникового зонда, причем крутизна преобразования растет с увеличением частоты ϖ0.
Известно, что глубина проникновения переменного электромагнитного поля зависит от его частоты. Критическую частоту, при которой это изменение становится существенным, можно оценить из выражения для комплексной глубины проникновения [5]:
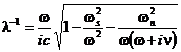 ,
,
где ϖs, ϖn - плазменные частоты сверхпроводящих и нормальных электронов, их значения порядка 1010 … 1011 Гц, ν - эффективная частота столкновений, равная 1010 Гц, ϖ - частота электромагнитного поля. Таким образом, изменение глубины проникновения в ![]() происходит на частоте порядка 1011 Гц и для рабочей частоты 30 МГц ей можно пренебречь. При низких температурах легко получить для контура, содержащего n = 100 витков добротность Q = 103. Если j0/jC = 0,9, тогда коэффициент пропорциональности между магнитным потоком Фn = SH, измеряемого поля, и амплитудой U0 выходного напряжения составит 1012 с-1.
происходит на частоте порядка 1011 Гц и для рабочей частоты 30 МГц ей можно пренебречь. При низких температурах легко получить для контура, содержащего n = 100 витков добротность Q = 103. Если j0/jC = 0,9, тогда коэффициент пропорциональности между магнитным потоком Фn = SH, измеряемого поля, и амплитудой U0 выходного напряжения составит 1012 с-1.
Собственное шумовое напряжение измерительного усилителя, приведенное к входу, имеет величину порядка 1 нВ в полосе 1 Гц, тогда порог чувствительности криозондового магнитометра по магнитному потоку ![]() не уступает лучшим сквидам, притом, что конструкция сверхпроводникового зонда гораздо проще и технологичнее. По сути, сверхпроводниковый зонд очень похож на криотрон, в котором вентиль является зондом, а управляющая катушка – резонансным контуром [4].
не уступает лучшим сквидам, притом, что конструкция сверхпроводникового зонда гораздо проще и технологичнее. По сути, сверхпроводниковый зонд очень похож на криотрон, в котором вентиль является зондом, а управляющая катушка – резонансным контуром [4].
Требование R << λ фактически использовалось только для упрощения расчетов. При практических применениях достаточно выбирать R ≈ λ, в этом случае взаимодействие скрещенных полей будет происходить по всему объему сверхпроводника. При этом для магнитометрии нужны "плохие" сверхпроводники – с большой глубиной проникновения и малой плотностью критического тока, например ВТСП-керамика с пониженным содержанием кислорода вблизи перехода. При температуре 77 К эффективная глубина проникновения в керамическом сверхпроводнике порядка 100 мкм [7].
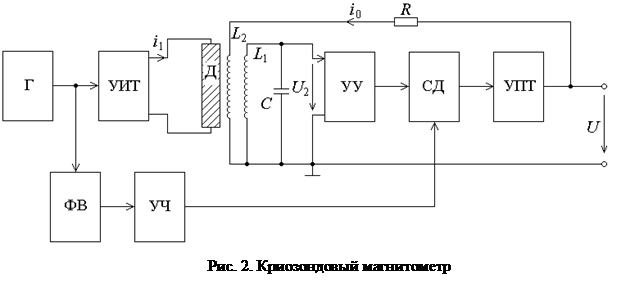
Структурная схема магнитометра с криозондовым датчиком, использующего нелинейное взаимодействие скрещенных магнитных полей, приведена на рис. 2. Основой магнитометра является сверхпроводящий датчик Д, через который пропускается переменный ток. Сигнал с генератора напряжения Г подается на управляемый источник тока УИТ, создающий в сверхпроводящем криозонде переменный ток i1 с частотой ϖ0. Напряжение второй гармоники U2 на сигнальной катушке L1 подается на узкополосный усилитель УУ, настроенный на частоту 2ϖ0, сигнал с его выхода поступает на синхродетектор СД, опорный сигнал на который подается от генератора через фазовращатель ФВ и удвоитель частоты УЧ. С выхода синхродетектора сигнал поступает на усилитель постоянного тока УПТ, выход которого через резистор R соединяется с катушкой L2, намотанной поверх сигнальной L1 катушки, замыкая цепь отрицательной обратной связи по магнитному полю. Напряжение на выходе U пропорционально величине внешнего магнитного поля Не с учетом знака.
Поскольку в соответствии с формулой (17) поток переменного магнитного поля через сечение сверхпроводника не зависит от направления тока в нем, сверхпроводящую проволоку диаметром 0,1 мм можно уложить "змейкой" так, чтобы в соседних звеньях ток протекал в противоположных направлениях. Зонд магнитометра диаметром 1 мм будет состоять из 100 таких звеньев и позволит получить порог чувствительности по магнитному полю порядка ![]() . Такая чувствительность является рекордной даже для квантовых магнитометров и позволит проводить предельные измерения в области гео- и био-магнетизма. В отличие от сквидов сигнальная характеристика криозондового магнитометра не является периодической, поэтому такой магнитометр может измерять абсолютное значение магнитной индукции, а не только ее изменение.
. Такая чувствительность является рекордной даже для квантовых магнитометров и позволит проводить предельные измерения в области гео- и био-магнетизма. В отличие от сквидов сигнальная характеристика криозондового магнитометра не является периодической, поэтому такой магнитометр может измерять абсолютное значение магнитной индукции, а не только ее изменение.
Таким образом, полученное приближенное решение задачи о взаимодействии взаимно-перпендикулярных магнитных поле в сверхпроводящей проволоке позволяет оценить предельную чувствительность сверхпроводящего магнитометра на основе эффекта взаимодействия магнитных полей в сверхпроводящей проволоке.
Работа выполнена в рамках реализации ФПЦ «Научные и научно-педагогические кадры инновационной Росии» на 2009 – 2013 годы (соглашение № 14.В37.21.0736).
Список литературы:
-
1.Горелик Г.С. О некоторых нелинейных явлениях, происходящих при суперпозиции взаимно перпендикулярных магнитных полей [Текст]// Известия Академии наук СССР, Серия Физическая, 1944. Т. VIII. - № 4. - С. 172 - 188.
2.Зацепин Н.Н. Метод высших гармоник в неразрушающем контроле металлов [Текст]: Монография/ Н.Н. Зацепин. - Мн: Наука и техника, 1980. - 167 с.
3.Игнатьев В.К., Якимец А.Л. ВТСП-магнитометр с двойной модуляцией [Текст]// Измерительная техника, 2000. - № 10. - С. 49 - 52.
4.Интегральные схемы и микроэлектронные устройства на сверхпроводниках [Текст]: Монография/ В.Н. Алфеев, П.А. Бахтин, А.А. Васенков и др.; Под ред. В.Н. Алфеева. - М.: Радио и связь, 1985. - 232 с.
5.Гинзбург В.Л., Ландау Л.Д. К теории сверхпроводимости [Текст]// Журнал экспериментальной и теоретической физики, 1950. Т. 20. Вып. 12. - С. 1064 - 1082.
6.Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям [Текст]: Монография/ В.Ф. Зайцев, А.Д. Полянин. - М.: Физматлит, 2001. - 576 с.
7.Я.В. Копелевич, В.В. Леманов, А.Л. Холкин. Частотная зависимость импеданса и глубина проникновения магнитного поля в керамике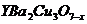 [Текст]// Физика твердого тела, 1989. Т. 31. - Вып. 8. - С. 302 - 304.
[Текст]// Физика твердого тела, 1989. Т. 31. - Вып. 8. - С. 302 - 304.