Степень реализации диаграммы деформирования бетона во внецентренно сжатых стойках

Аннотация

В.А. Мурадян

Дата поступления статьи: 25.09.2013

На основании опытных данных о сопротивлении железобетонных колонн внецентренному сжатию была получена аналитическая зависимость предельной сжимаемости бетона от варьируемых факторов: относительного эксцентриситета внешней силы eo /h и процента армирования µ.  

Ключевые слова: железобетонная колонна, продольная арматура, защитный слой бетона, метод конечных элементов, критическая нагрузка

Была поставлена задача на основании опытных данных о сопротивлении железобетонных колонн внецентренному сжатию получить аналитическую зависимость предельной сжимаемости бетона от варьируемых факторов: относительного эксцентриситета внешней силы e_o /h и процента армирования µ. К анализу кроме опытных данных автора были привлечены и данные РГСУ [1, 9].
Эта задача была разбита на две подзадачи:

• нахождение функциональной зависимости ε_bu от относительного эксцентриситета приложения внешней силы e_o /h;
• нахождение функциональной зависимости ε_bu от e_o /h и от процента армирования µ

На первом этапе необходимо было определить структуру эмпирических формул, заданных в следующем виде:
ε_bu = ʄ (e_o /h, β₁, β₂,…, β_k)    (1)                                     
β_i = g_i (µ, α₁, α ₂,…, α _k), i =0, 1, 2,…, k  (2)                             
α_i = h_i (, γ₁, γ ₂,…, γ _k), i =0, 1, 2,…, k   (3)                            
где αi, βi и γi – параметры получаемых формул.
Подставляя последовательно выражение (3) в (2) в (1) получаем искомую функциональную зависимость:
ε_bu= F (e_o /h, µ, , γ₁, γ ₂,…, γ _k)  (4)                               
Практическое осуществление вышесказанного осуществлялось следующим образом. Рассмотрим формулу (1). Так как экспериментальные зависимости ε_bu от e_o /h имеют некоторый разброс, то система уравнений:
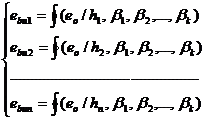        (5)                              
Является как правило несовместной. Поэтому необходимо было найти наилучшие значения параметров β₁, β₂,…, β_k, приближенно удовлетворяющие системе уравнений (5), т.е. минимизирующие невязки:
   (6)                              
При анализе был использован метод наименьших квадратов, согласно которому наилучшими оценками параметров β₁…β_kсчитаются те, для которых сумма квадратов отклонений
S(β₁, β₂,…, β_k) =     (7)                               
Будет минимальной. В формуле (7) S(β₁, β₂,…, β_k) функция многих переменных. Используя необходимые условия экстремума для функции многих переменных, получим систему уравнений для определения β₁, β₂,…, β_k:
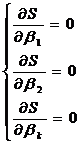      (8)                                           
Получение требуемой эмпирической формулы состояло из двух этапов: определения общего вида этой формулы и нахождения ее параметров, удовлетворяющих системе уравнений (8).
Установлено, что кривая, описываемая формулой
   (9)                                        
наилучшим образом совпадает с кривой, построенной по экспериментальным данным. Параметры этой формулы а, в, с найдены решением системы(8).
Для полученных параметров формулы (9) а, в, с найдены аналогичным образом следующие функциональные зависимости от процента армирования µ:
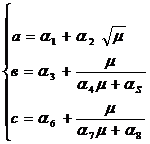 (10)                                     
Подставив эти выражения параметров в формулу (7), получим функциональную зависимость ε_bu бетона от эксцентриситета приложения внешней силы e_o /h и процента армирования µ, в виде
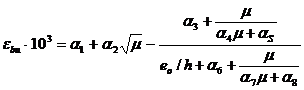  (11)                    
Зависимость (11) получена для образцов с прочностью бетона = 25-30 МПа, т.е. параметры  α₁, α₂,…, α ₈ в (10) вычислены для определенной прочности бетона (табл. 1).
По табл. 1 можно находить значения коэффициентов α_i для дальнейшего определения ε_bu.
Таблица 1
Значение параметров α_i формулы (11) для прочности бетона 25-30 МПа

Формула (11) справедлива для ненапряженных в нецентренно сжатых элементов из тяжелого бетона при = 25-30 МПа. С математической точки зрения при µ=0 или e_o /h=0 происходит деление на ноль, что приводит к неопределенности. Поэтому в этих случаях, т.е. когда µ=0 или e_o /h=0 будем считать значения последних бесконечно малыми величинами.
Отклонения опытных данных ε_bu от вычисленных по предлагаемым формулам (11) невелики, они не превышают 4,2%.

Литература:

1. Бойцов В.Н., Маилян Д.Р. Рекомендации по расчету внецентренносжатых предварительно напряженных железобетонных элементов геометрической гибкостью 10-60 из тяжелого бетона и высокопрочной арматуры. - Ростов-на-Дону: Ростовский ПромстройНИИпроект,1984.-22с.
2. Гуща Ю.П. Об учете неупругих деформаций бетона и арматуры в расчете железобетонных конструкций по первой и второй группам предельных состояний// Совершенствование конструктивных форм, методов расчета и проектирования железобетонных конструкций. Сборник научных трудов. –М.: НИИИЖБ,1983.- С.11-18.
3. Дмитриев А.В. Динамический расчет изгибаемых железобетонных элементов при действии изгибающих моментов и продольных сил// Бетон и железобетон. – 1996. - №5. – с.16-19.
4. Мурадян В.А., Маилян Д.Р. К методике расчета железобетонных внецентренно сжатых колонн // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1333 (доступ свободный) – Загл. с экрана. – Яз. рус.
5. Карпенко Н.И., Мухамедиев Т.А. К расчету  прочности нормальных сечений изгибаемых элементов // Бетон и железобетон. – 1983. - №4. – С.11.
6. Лемыш Л.Л. Провести исследование несущей способности элементов типовых каркасных промзданий с более полным учетом особенностей работы бетона и разработать рекомендации по их расчету. Отчет ЦНИИ-промзданий. –М.,1982. – С.47-49.
7. Маилян Д.Р., Несветаев Г.В. Зависимость относительной несущей способности колонн от относительного эксцентриситета// «Инженерный вестник Дона». - 2012. – №4-2. -183с. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1334 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Mkrtchyan A., Akcenov V., Mailyan. Experimental study of the structural properties of high-strength concrete // 5th International Scientific Conference “European Applied Sciences: modern approaches in scientific researches”:Papers of the 5th International Scientific Conference. August 26–27. - Stuttgart, Germany. – 2013.  - 164 p.
9. Маилян Д.Р. Расчет преднапряженных гибких железобетонных колонн по деформированной схеме// Вопросы прочности, деформативности и трещиностойкости железобетона, вып. 8. – Ростов-на-Дону,1980. – С.32-35.
10.  Mkrtchyan A., Akcenov V., Mailyan. Experimental study of reinforced concrete columns of high-strength concrete // “Applied Sciences and technologies in the United States and Europe: common challenges and scientific findings”: Papers of the 2nd International Scientific Conference (September 9–10, 2013). Cibunet Publishing. - New York, USA. - 2013. - 242 p.