Аналитическое описание диаграммы деформирования высокопрочных бетонов

Аннотация

А.М. Мкртчян, В.Н. Аксенов

Дата поступления статьи: 25.08.2013

В статье предложена новая зависимость для аналитического описания диаграммы «b–b» высокопрочных бетонов классов В70…В110. Формула разработана на основе принятой в Европе зависимости Сарджина и хорошо согласуется с полученными экспериментальными данными. Разработана новая зависимость предельных относительных деформаций бетона на сжатие от его прочности.

Ключевые слова: высокопрочный бетон, физический эксперимент, диаграмма состояния бетона, зависимость напряжения-деформации в бетоне, предельные относительные деформации бетона

С введением в 2003 году новых норм [1, 2] основным методом расчета в России и странах СНГ стал считаться расчет по нелинейной деформационной модели с использованием диаграмм состояния бетона и арматуры. Однако авторы норм предложили инженерам использовать только упрощенные зависимости, в которых реальная криволинейная диаграмма «σ_b–ε_b» аппроксимируется набором линейных функций, состоящих из двух или трех участков. Исследования полных диаграмм деформирования для тяжелых бетонов средней прочности проводятся в нашей стране и сейчас [3, 4].
Вопросам аналитического описания диаграмм деформирования бетонов посвящено большое количество исследовательских работ за рубежом [5, 6, 7, 8]. Исследователи предлагают новые зависимости или корректируют известные ранее. Из множества предложений в качестве основной диаграммы европейский комитет по железобетону (далее ЕКБ-ФИП) назвал зависимость Сарджина [9], включенную также в европейские нормативные документы [10]. Зависимость имеет вид:
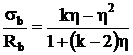,   (1)
где
η=ε_b/ε_b0,                                                                                                  
.                                                                                       
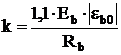Ее применимость для бетонов средней прочности (В15…В60) подтверждена многочисленными опытами.
Проведенные в России исследования работы конструкций, выполненных из высокопрочных бетонов , не давали необходимых данных для анализа полной диаграммы «σ_b–ε_b». С целью изучения возможности применения формулы (1) для описания деформирования высокопрочных бетонов классов выше В60 были проведены экспериментальные исследования.
Были изготовлены бетонные призмы размерами 100х100х400 мм из бетонов классов В65…В110. Образцы испытывались в гидравлическом прессе в соответствии с ГОСТ [12]. Одной из задач исследования являлось получение экспериментальных данных, необходимых для построения диаграмм деформирования бетона в условиях центрального сжатия при кратковременном действии нагрузки с учетом нисходящей ветви.
Экспериментальные диаграммы состояния бетона «σ_b–ε_b» при сжатии от действия кратковременной нагрузки приведены на рис. 1. Деформации сжатия здесь и далее условно приняты положительными.

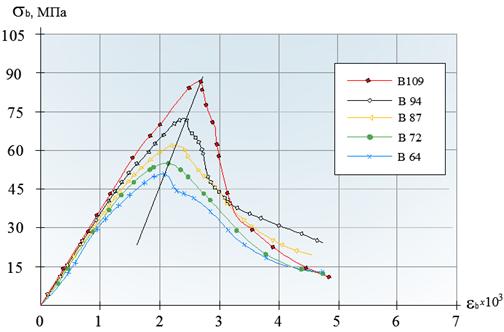
Рис. 1.- Экспериментальные диаграммы «σ_b–ε_b» для высокопрочных бетонов

На представленных графиках следует заметить, что максимальная относительная деформация, ε_b0, соответствующая напряжению R_b, увеличивается с ростом прочности бетона. Несложно убедиться, что для исследуемых высокопрочных бетонов В70…В110 эта зависимость носит линейный характер. Для ее описания предлагается следующая формула:
εb0=(1,62 Rb+127,33)∙10 ^-5. (2)
Здесь Rb следует подставлять в МПа.
Построение диаграммы ЕКБ-ФИП по формуле (1) для исследуемых высокопрочных бетонов показало значительные расхождения теоретических кривых с данными эксперимента как в восходящей части диаграммы, так и в нисходящей (см. рис. 2). Принято решение о корректировке зависимости (1).

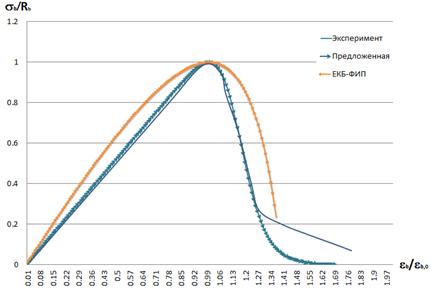
Рис. 2.- Диаграммы состояния бетона: экспериментальная, по предложенной формуле (3) и по формуле ЕКБ-ФИП (1)

Анализ различных математических функций показал, что диаграмма, построенная на основе предлагаемой зависимости (3) наиболее точно описывает форму экспериментальных кривых в восходящей части, а также в нисходящей части до напряжений σ_b≈(0,25…0,3)R_b.
 ,      (3)
где 
η=ε_b/ε_b0,                                                                                             
r=(Δ-0,5)R,                                                                                                 
R – прочность бетонного образца,
Δ – коэффициент упругости в вершине диаграммы, определяемый по формуле
Δ=   или   Δ=,                                                                    
где    E₀ –модуль деформации бетона в вершине диаграммы, соответствующий тангенсу угла, α₀, наклона секущей к кривой σ_b–ε_b в точке с относительными деформациями ε_b=ε_b0 (рис. 3). Графически E₀= R_b/ε_b0,
E_b – начальный модуль упругости бетона,
ε_b0 рекомендуется определять по предложенной формуле (2).

     Рис. 3.- К определению Е₀

На основе анализа экспериментальных и теоретических данных для аналитического описания диаграммы деформирования высокопрочных бетонов классов В70…В110 рекомендуется использовать зависимость (3). Учитывать рост предельных относительных деформаций бетона на сжатие с увеличением его класса предлагается по зависимости (2).

Литература:

1. СНиП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения [Текст].– Введ. 2004-03-01. –М.: ФГУП ЦПП, 2004. – 24 с.
2. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры. [Текст] .– Введ. 2004-03-01. – М.: ФГУП ЦПП, 2004. – 54 с.
3. 3. Кургин, К.В., Маилян Д.Р. О необходимости трансформации базовой аналитической зависимости "sb–eb" бетона. [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2011/712 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Маилян, Д.Р., Несветаев, Г.В. Зависимость относительной несущей способности колонн от относительного эксцентриситета. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1334 (доступ свободный) – Загл. с экрана. – Яз. рус.
5. Metin Husem, Selim Pul. Investigation of stress–strain models for confined high strength concrete [Текст] // “Sadhana” Vol. 32, Part 3, June 2007, pp. 243–252. – India.
6. El-mahadi, A. Rheological Properties, Loss of Workability and Strength Development of High-Strength Concrete [Текст] / El-mahadi Ahmed.– London: MSc. University of London, 2002. – 144 р.
7. Mehdi Sadeghi e Habashi. Ultra high performance and high early strength concrete [Текст] // “36th Conference on Our World in Concrete & Structures” , pp. 56–68.  –  Singapore, 2011.
8. Cusson, D., Paultre, P. Stress–strain model for confined high-strength concrete [Текст] //. J. Struct. Eng. 121, pp. 468–477. – London, 1995.
9. Comite Euro-International du beton. CEB-FIP model code (Design code) [Текст].– Paris: Thomas Telford, 1990. – 437 р.
10. EN 1992 Eurocode 2: Design of concrete structures. Part 1: General rules and rules for buildings [Текст].– Brussels: European Committee for Standardization, 2001. – 52 р.
11. ГОСТ 24452-80. Бетоны. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона [Текст].– Введ. 1982-01-01.–М.: ФГУП «Стандартинформ», 2005. –12 с.