Адаптивные автономные сценарии в задачах управления информационными ресурсами предприятия

Аннотация

В.А. Филатов, В.А. Кривоносов, О.Ф. Козырь

Дата поступления статьи: 01.08.2013

Рассматривается проблема использования адаптивных автономных сценариев в решении задач управления информационными ресурсами вычислительных систем. Разработана концептуальная модель адаптивного автономного сценария с использованием фреймов и аппарата конечных автоматов, что расширяет возможности автоматизации сложных задач управления информационными ресурсами.  

Ключевые слова: адаптивные автономные сценарии, теория конечных автоматов, фрейм, слот, управление распределенными информационными ресурсами.

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Введение

В соответствии с современными тенденциями управления информационными ресурсами (УИР) и развития информационных услуг [1] целесообразно создание инструментария УИР, способного  адаптироваться к быстро меняющимся условиям функционирования, интегрировать различные технологии и системы,  координировать все множество используемых приложений. В качестве такого инструментария может быть использована технология автономных сценариев (АС) [2, 3], обладающая рядом преимуществ, таких как независимость от сред и платформ реализации, от квалификации разработчика, гибкость и сравнительная  универсальность применения. Сферу применения автономных сценариев   можно расширять вплоть до выполнения интеллектуальных заданий.

В работах [2, 3] рассмотрены модели автономных сценариев и их поведения в информационной среде, которые облегчают проектирование, сопровождение и мониторинг текущего состояния АС в процессе управления информационными ресурсами. В зависимости от характера решаемых задач АС могут различаться по структуре и степени автономности функционирования в информационно-вычислительной среде [2].

Структура модели адаптивного автономного сценария

Автоматизированное решение задач, в которых должен быть достигнут конкретный результат (например, регулярное создание резервных копий архива), возможно посредством адаптивного автономного сценария (ААС),  способного изменять алгоритм своей работы в зависимости от происходящих  в системе событий. С целью построения и обоснования архитектуры адаптивного автономного сценария необходимо исследование как структурных, так и поведенческих его аспектов. Это предполагает разработку формализованного описания сценария.

Для формализации структуры адаптивного автономного сценария может быть использована фреймовая модель [4], являющаяся дальнейшим развитием подхода, рассмотренного в [2,5-7]. Автономный сценарий рассматриваемого класса представляет собой набор слотов-кортежей, каждый из которых описывает свой вариант действия ААС. Слот-кортеж имеет уникальный идентификатор ID (ключевой атрибут), может быть связан со своим объектом информационного пространства и выполнять с ним действие, заданное спецификацией оператора [ACT]. Выполнение действия ограничено условиями, задаваемыми в опции  [CON]. Результат выполнения действия отражается в кортежах-состояниях {R}_ij слота задания. Конфликтные ситуации между выполняемыми заданиями (или сценариями) разрешаются на основе приоритетов, заданных в поле [PRI]. Логическая модель структуры ААС представлена на рис. 1.

Запишем формализованное представление структуры слота [8]:

                              Slot =〈U, D, dom, ri,  θ, Ω〉,                                 (1)

где U = {ID, PRI, OBG, CON, ACT, FLAG} –  множество имен атрибутов, D –  множество доменов,   dom –   отображение U ⇒ D, θ – множество, определяющее начальные условия и признаки   выполнения действий в структуре задания, r_i –  модель-кортеж  i-го слота автономного сценария, Ω – множество операций (над слотами-кортежами,   над состояниями кортежей,  над значениями типовых атрибутов).

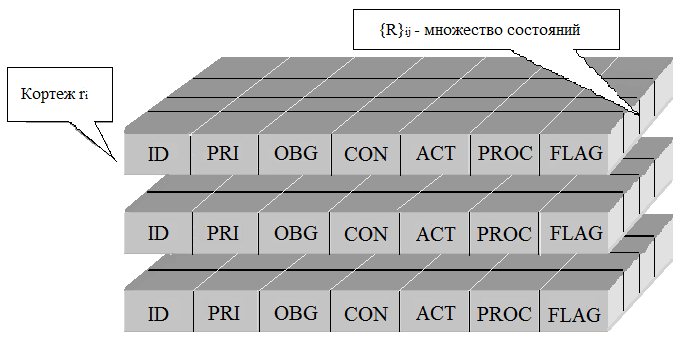
Рис.1. Логическая модель структуры ААС

Кортеж r_i в модели (1) представлен в виде:

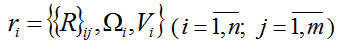                                                            (2)          

где {R}_ij – множество состояний кортежа r_i, V_i –множество ограничений целостности, Ω_i ⊂ Ω –  множество операций, заданных на  {R}_ij,  n  количество слотов-заданий, m  количество состояний i-го кортежа-задания.

Модель адаптивного поведения автономного сценария

Для  моделирования адаптивного поведения автономного сценария применим аппарат конечных автоматов [9,10]. При этом сценарий рассматривается как некоторый объект, способный в каждый момент времени  t = 0,1,2,…,N воспринимать конечное число сигналов s₁, s₂,…,s_K от информационной среды и изменять в зависимости от них выполняемое действие f ∈ (f₁, f₂,…, f_n). Каждое  действие f_i автономного сценария  вызывает ответные реакции s₁, s₂,…,s_K информационной среды E, в которой  находится сценарий. Эти реакции, в свою очередь, являются входными сигналами для принятия решения об изменении внутреннего состояния  φ ∈ ( φ₁,  φ₂,…,  φ_m) автономного сценария, определяющего его дальнейшее действие f_i+1.

На основе вектора реакций s₁, s₂,…,s_K информационной среды сформируем скалярную оценку S = F( s₁, s₂,…,s_K) действия автономного сценария. В простейшем случае оценка S представляет собой двоичную величину: либо S=1 - (действие удачно), либо S=0 -  (действие неудачно). В более сложном случае оценка – дробная величина, лежащая в интервале (0 – 1). При этом и в первом и во втором случае величина S характеризует степень результативности, а (1-S) - степень «бесполезности» действия стохастического автономного сценария.

Целесообразность поведения автономного сценария в информационной среде заключается в увеличении числа благоприятных реакций и уменьшении числа реакций неблагоприятных.

Поведение автономного сценария задается уравнением f(t)=F(φ(t)), описывающим зависимость действия f(t) автомата в момент t от его состояния φ(t), и матрицами ||a_ij(S)||, ||a_ij(1-S)|| i,j ∈ (1,2,…,m), управляющими изменением состояния φ(t) автономного сценария на основе оценки S его предыдущего действия. При этом элементы матрицы ||a_ij(S)|| показывают степень целесообразности перехода из состояния φ_i в состояние φ_j при удачном действии АС на предыдущем шаге. Матрица ||a_ij(1-S)|| показывает степень целесообразности перехода из состояния φ_i в состояние φ_j при неудачном действии АС.

Выбором оценки S и матриц ||a_ij(S)||, ||a_ij(1-S)|| можно реализовать различные стратегии адаптации поведения автономных сценариев. Если все элементы матриц ||a_ij(S)||, ||a_ij(1-S)|| выбрать так, чтобы они удовлетворяли условиям

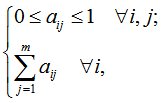                                                        (3)

то значения a_ij матриц ||a_ij(S)||, ||a_ij(1-S)|| можно трактовать как вероятности перехода из состояния φ_i в состояние φ_j при удачном и неудачном действии автономного сценария на предыдущем шаге соответственно.

Рассмотрим подробнее простейший случай, когда оценка S действий ААС является двоичной величиной S∈{0,1}. При этом каждая i-я строка матриц ||a_ij(1)||, ||a_ij(0)|| содержит по одному единичному значению. Единичное значение элемента a_ij(1) показывает, что из состояния φ_i ААС перейдет в состояние φ_j при удачном действии. Соответственно единица в элементе a_ij(0) задает переход из состояния φ_i в состояние φ_j при неудаче ААС на предыдущем этапе.

В адаптивных автономных сценариях могут быть реализованы два варианта изменения состояния:

- детерминированный, когда матрицы |a_ij(1)||, ||a_ij(0)||, сформированные разработчиком ААС, не изменяются в процессе его эксплуатации;

- рандомизированный, когда неудачное действие из состояния φ_i приводит к изменению положения 1 в i-й строке соответствующей матрицы. Новое положение 1 определяется с использованием генератора случайных чисел.

Анализ двух матриц переходов |a_ij(1)|| и ||a_ij(0)|| и логической модели фрейма-сценария, представленных на рисунке 2, показывает, что в случае применения обобщенной интегрированной структуры фрейма-сценария можно создать одну обобщенную модель, отражающую как структуру, так и поведение ААС.

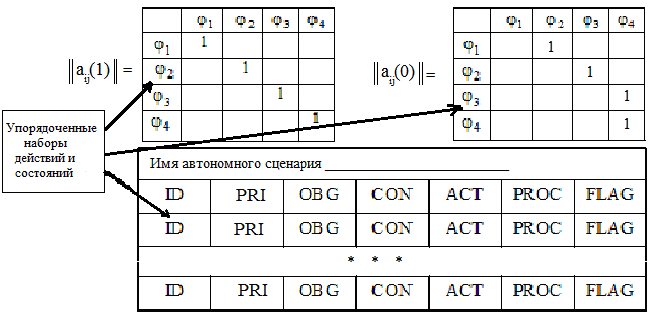
Рис. 2. Структура фрейма и матриц переходов ААС

Такая функциональная логическая модель фрейма ААС будет включать атрибуты: ID  ключевой атрибут слота-кортежа; PRI – приоритет выполняемого слотом задания, используемый для регулирования отношений между выполняемыми заданиями; S1  атрибут, значениями которого являются указатели слота-кортежа, на который передается управление, если реакция после выполнения данного действия положительна; S0  атрибут, значениями которого являются указатели слота-кортежа, на который передается управление, если реакция после выполнения данного действия отрицательна; атрибуты фиксированного набора  {OBG, CON, ACT, PROC, FLAG}.

Таким образом, модифицированная схема слота в структуре фрейма ААС, представленная на рисунке 3, имеет на два служебных атрибута больше, чем обычная схема.

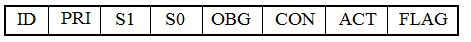
Рис.3 Модель модифицированного слота ААС

Рассмотрим на примере модель поведения автономного сценария такого класса. Сценарий должен выполнить три взаимосвязанных действия f₁, f₂, f₃. Матрицы переходов   |a_ij(1)|| и ||a_ij(0)|| имеют следующий вид:

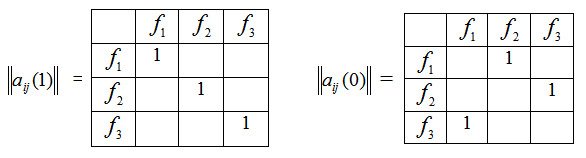
Алгоритм ААС состоит в следующем: задание (выполнение действия f₁), сформулированное в первом слоте-кортеже, выполняется столько раз, пока не изменится реакция S информационной среды на это действие 1→0. При таком изменении параметра S управление передается на второй слот-кортеж. Действие f₂ сменится на действие f₃, тоже только при изменении S =1→0.

Таким образом, мы получили по Цетлину [10] объект с «недоверчивой» манерой поведения. Как только реакция на действие отрицательна, тип действия изменяется, при положительной реакции объект остается в предыдущем состоянии.

Компактно в терминах разработанной модели автономного сценария логическая схема выглядит следующим образом (рисунок 4).

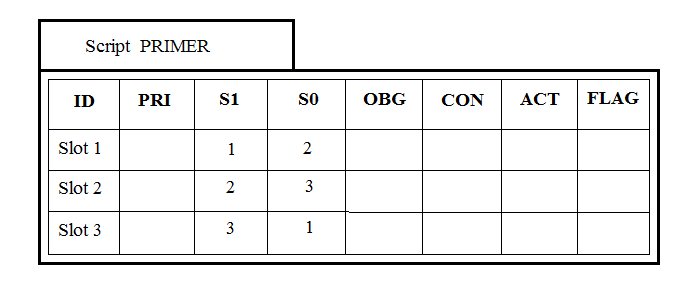
Рис.4. Логическая модель ААС

Отличие сценариев данного класса состоит в том, что обрабатываться могут данные межоперационных состояний, хранящихся в кортежах-состояниях отношений r_i, i=1,2,…,n.  

Рассмотрим адаптивный автономный сценарий, который выполняет следующие действия. Он посылает в сообщении серверу размер передаваемых файлов (временной папки D:\ResDir) SizeFiles. Это сообщение активизирует на сервере процедуру DeleteFile.exe, которая  сравнивает полученное  значение с размером свободной памяти сервера БД. И если памяти не достаточно для сохранения всех файлов пользователя, находящихся во временной папке D:\ResDir\,  то производит поиск и удаление в папке D:\arhiv и вложенных в нее папках всех файлов, сохраненных более недели назад. И снова проверяет, достаточно ли места для передачи файлов пользователя на сервер. Если и в этот раз памяти не достаточно, то управление передается администратору сети, то есть вызывается программа  Dialog.exe,  предоставляющая администратору интерфейс и доступ к  инструментам для решения возникшей проблемы. Иначе передает ответное сообщение пользователю, которое запускает для передачи файлов на сервер пользовательскую функцию GetFiles().

Функция GetFiles() подтверждает факт удачного сохранения файлов на сервере выдачей пользователю соответствующего сообщения или указывает на произошедший в сети сбой. Ее также можно реализовать в виде автономного сценария  и при необходимости сохранять результаты переноса файлов пользователя в специальном журнале, представляющем собой либо таблицу БД, либо текстовый файл.

Такой ААС может быть представлен в виде таблицы СУБД, схема которой приведена на рисунке 5.  

Рис.5. Схема таблицы СУБД, описывающей ААС

Часть функций программного сценария  выполняется на ПК пользователей, таких как передача размера временной папки с файлами на сервер, получение разрешающего передачу сообщения, передача файлов на сервер, а также получение  сообщения о благополучном сохранении файлов на сервере или  сбоя в работе сети. Другая часть функций, таких как проверка достаточного   количества свободной памяти диска, удаление неактуальных данных, отправка пользователю разрешения на передачу файлов или предупреждения администратору о переполнении  сервера - на сервере. Передача управления между сценариями производится посредством системных сообщений. Для передачи управления автономным сценариям, выполняющимся на разных ПК, серверах или в разных сегментах корпоративной сети кроме сообщений можно использовать также сигналы с различных устройств (ПК, контроллеров, мобильного телефона, датчика инфракрасного излучения и др.).

Заключение

В статье рассмотрены вопросы построения модели  адаптивного автономного сценария, ориентированного на управление информационными ресурсами корпоративных вычислительных систем.  Формальный подход к построению модели основан на концепции фреймов и теории конечных автоматов. Предложенный подход может эффективно применяться для разработки систем управления корпоративной информацией и решения широкого круга задач управления распределенными информационными ресурсами.

Библиографический список:

1. Радчук В.А. Закономерности развития рынка информационных услуг на современном этапе (обзор) [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2011/494/ (доступ свободный) – Загл. с экрана. – Яз. рус.  

2. Козырь О.Ф. Разработка концептуальной модели автономного сценария управления информационными ресурсами [Текст] // Материалы IV Всероссийской открытой научно-практической конференции «Актуальные задачи ММиИТ» 22-27 мая 2010 – Сочи: СГУТиКД

3. Филатов В.А., Козырь О.Ф. Модель поведения автономного сценария в задачах управления распределенными информационными ресурсами [Электронный ресурс] / «Инженерный вестник Дона», 2013, № 3 -Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/ (доступ свободный) – Загл. с экрана. – Яз.рус.

4. Minsky, Marvin. A framework for representing knowledge. [Electronic resource] // MIT AI Laboratory Memo 306.  June, 1974. -. Режим доступа: http://web.media.mit.edu/~minsky/papers/Frames/frames.html (доступ свободный) – Загл. с экрана. – Яз. англ.  

5. Филатов В.А. Модель поведения автономного агента на основе теории автоматов [Текст] // Вестник Херсонского государственного технического университета. - Херсон: ХГТУ, 2004 - № 1 (19) - c. 108-111.

6. Филатов В.А., Козырь О.Ф. Логическая модель программного агента в задачах управления информационными ресурсами вычислительных систем [Текст] // Образование, наука, производство и управление в ХХ1 веке. Сборник трудов Международной научной конференции. в 4-х томах. - Старый Оскол: ООО "ТНТ", 2004 - том 4 - с.357-361.

7. Филатов В.А., Козырь О.Ф. Мультиагентный подход к идентификации пользователей в системе дистанционного образования [Текст] // Образование, наука, производство и управление. Сборник трудов региональной научной конференции. в 2-х томах. - Старый Оскол ООО "ТНТ", 2005 - том 1- с.284-290.

8. Codd E.F. Extending the Database Relational Model to Capture More Meaning [Text] // Journal “ACM Transactions on Database Systems”, NY, USA: TODS Homepage “ACM Trans. Database Syst.”,  1979, № 4,  – p. 397 - 434.

9. Варшавский В.И. Коллективное поведение автоматов [Текст] // В.И. Варшавский  М.: "Наука",  Главное издательство физико-математической литературы,  1973  408 с.

10. Цетлин М. Л.  Исследования по теории автоматов и моделированию биологических систем  [Текст] // М.Л. Цетлин  М.: "Наука", 1969  с.316