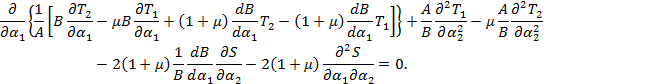Соотношения между компонентами поверхностной нагрузки в оболочках вращения при безмоментном их состоянии
Аннотация
На основании уравнений равновесия элемента оболочки по безмоментной теории и уравнений неразрывности её срединной поверхности получены соотношения между компонентами поверхностной нагрузки в оболочках вращения. Эти соотношения удобны для перехода к частным случаям оболочек вращения при их осесимметричном исходном докритическом состоянии.
Ключевые слова: оболочка вращения, безмоментное состояние, компоненты поверхностной нагрузки
1.Основные уравнения.
При исследовании общей устойчивости оболочки следует, очевидно, считать, что последняя до наступления критического состояния не должна испытывать даже бесконечно малых изгибаний, так как потеря общей устойчивости предполагает смену форм равновесия. Такими формами равновесия могут быть: безмоментная начальная форма при отсутствии бесконечно малых изгибаний и моментная-после потери устойчивости. Очевидно также и то, что указанное исходное состояние оболочки возможно лишь при тангенциальных граничныхусловиях и наложении некоторых ограничений на поверхностную нагрузку или на её компоненты вдоль координатных осей 
ибо деформация оболочки без изгиба возможна только при определенных соотношениях этих компонент. Отсюда возникает вопрос отыскания этих соотношений при дальнейшем определении критических значений нагрузок
Имея же набор нагрузок, соответствующих безмоментному напряженному состоянию оболочек, и зная их критические значения, интересно сравнить эти нагрузки с заданными. Из заданных нагрузок всегда можно выделить ту их часть, которая способствует безмоментному состоянию оболочки. И если выделенная часто нагрузок близка к своим критическим значениям, то даже небольшое отличие заданных нагрузок от выделенной их части будет вызывать значительные деформации оболочки, учесть которые может лишь нелинейная теория оболочек.
Однако, если выделенная часть нагрузок далека от своих критических значений, деформации оболочки будут невелики. А это означает правомерность использования в таком случае более простой и удобной линейной теории оболочек. Установить этот факт и представляет, на наш взгляд, в дальнейшем наибольший интерес.
Все последующие выкладки построены на основе допущений теории Кирхгофа для тонких оболочек. В качестве исходных приняты уравнения равновесия элемента оболочки по безмоментной теории, что соответствует деформации оболочки без изгиба, и уравнения неразрывности срединной поверхности оболочки так же для случая безмоментной работы последней[1].
Уравнения равновесия:
(1)
Уравнения неразрывности срединной поверхности:
(2)
Здесь 
-- криволинейные координаты, относящиеся к точкам срединной поверхности оболочки, котораяможет быть задана радиус-вектором
параметрыЛяме срединной поверхности оболочки;
главные радиусы кривизны срединной поверхности;
погонные усилия растяжения-сжатия элемента срединной поверхности оболочки в направлении соответствующих криволинейных координат;
погонное сдвигающее усилие, возникающее в срединной поверхности в направлении криволинейных координат;
коэффициент Пуассона.
Для отыскания необходимых соотношений между компонентами нагрузки имеем, таким образом, в общем случае систему из 6 уравнений (1) и (2).
Исключая из этих уравнений усилия
можно получить для конкретной оболочки искомые соотношения между компонентами нагрузки
Уместно заметить, что опирание оболочки предполагается исключающим всякую возможность её изгиба на опорах, то есть имеют место тангенциальные граничные условия.
2. Безмоментное состояние оболочек вращения.
Так как для оболочек вращения все геометрические характеристики являются функциями одной координаты (пусть
направленной по меридиану, то есть
кроме того, 
уравнения (1) и (2) упрощаются и после некоторых преобразований принимают вид:
|
|
(3) |
3. Оболочки вращения в безмоментном напряженном состоянии, симметричном относительно оси вращения.
Симметрия напряженного состояния оболочек вращения постулированно вытекает из симметрии нагрузки. В нижеследующем, однако,будем исходить из симметрии напряженного состояния, а не нагрузки, поскольку нашей целью является выявление соотношений между компонентами нагрузки. Симметрия напряженного состояния накладывает следующие условия на усилия, действующие по граням элемента срединной поверхности оболочки: 
В этом случае вместо уравнений (3) получаем:
(4)
И теперь имеем симметрию нагрузки, то есть
в чем легко убедиться.
Исключим из уравнений (4) усилия
Так как 
то, найдя из третьего уравнения
и подставив во второе, получим:
Это дифференциальное относительно 
удобно записать в виде
c известным решением 
(5)
Подставляя (5) в выражение для
получим:
(6)
Используя теперь (5) и (6) в двух последних уравнениях (4), получим после приведения подобных членов интересующие нас соотношения между компонентами нагрузки 
и 
(7)
где
Причем при
из двух уравнений (7) остается только первое уравнение, а второе является его следствием; при 
первое уравнение обращается в тождество, и вновь остается одно, на этот раз, второе уравнение.Постоянную интегрированияС легко можно найти, используя всякий раз граничные условия.
Литература:
1.Огибалов П.М., Колтунов М.А. Оболочки и пластины. М., Изд-во МГУ, 1969.