Исследование устойчивости неоднородных полимерных стержней в условиях термовязкоупругости
Аннотация
Результаты решения задач показали сильную зависимость физико-механических и релаксационных свойств полимера от температуры. Значительно сказывается на времени, в течение которого стержень способен сохранять устойчивое положение.
К примеру, стержень, нагруженный всего на 57% от Эйлеровой силы, теряет устойчивость при температуре примерно в 15 раз быстрее, чем при температуре . Таким образом, для полного использования потенциала полимерного материала необходимо защищать его от температурного воздействия.
Ключевые слова: тепловое нагружение, устойчивость, алгоритм, аппроксимация.Ключевые слова: тепловое нагружение, устойчивость, алгоритм, аппроксимация
Полимерные материалы обладают многими положительными качествами: кислото- и щёлочестойкость, высокая прочность на разрыв (у некоторых разновидностей полиметилметакрилата достигает 2000 МПа) и т.д. Однако полимерным материалам, как говорилось выше, присуще сильное проявление реологических свойств. Ситуацию усугубляет то, что все упругие и высокоэластические параметры полимеров очень сильно меняются в зависимости от температуры. Так, при нагреве образца из ПММА от 
до 
значение модуля начальной релаксационной вязкости 
уменьшается практически в два раза.
Таким образом, даже небольшой перепад температур в образце способен создать значительную косвенную неоднородность, которая самым неблагоприятным образом способна сказаться на работе конструкции.
Вывод основных разрешающих уравнений
При выводе основных уравнений предполагается, что на образец не действует температурное поле или температурное поле постоянно по оси стержня остаётся неизменным, т.е.
.
Однако значения физико-механических параметров материала имеют сильную зависимость от температуры, а следовательно, от координаты , к примеру для модуля упругости:
В работе[1]рассматривается жёстко закреплённый с обоих концов стержень под действием температурной нагрузки. Однако он не учитывает возможность приложения механической нагрузки.
Использованные в расчетах значения релаксационных констант, их зависимости от температуры для эпоксидной композиции ЭДТ-10 и полиметилметакрилата (ПММА) для «старшего» составляющего спектра приводятся в работе[2]:
При выводе разрешающих уравнений основные интегральные соотношения не меняются:
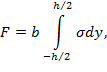(1)
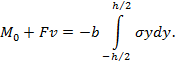(2)
В случае выполнения гипотезы плоских сечений запишется и выражение полных деформаций:
(3)
С другой стороны, с учетом температурных деформаций, можно записать:
(4)
где 
– температурные деформации.
С учетом (3) и (4) можно записать
(5)
Подставляя выражение (5) в (1) и проведя интегрирование, определяют осевые деформации стержня:
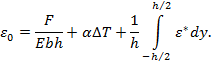(6)
Аналогичным образом после подстановки выражения (5) в (2):
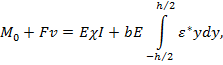(7)
где 
– осевой момент инерции стержня относительно оси 
.
С учетом того, что
, окончательное разрешающее уравнение для оси стержня принимает вид:
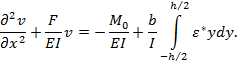(8)
Для удовлетворения произвольных граничных условий производится дважды дифференцирование выражения по 
. Однако теперь :
: (9)
Вводится обозначение: пусть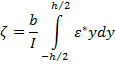 
, тогда выражение (9) принимает вид:
(10)
Таким образом, основное разрешающее уравнение представляет собой неоднородное дифференциальное уравнение четвертого порядка с переменными коэффициентами.
Методика и алгоритм решения нелинейных уравнений, численная реализация
Пусть на исследуемый стержень действует некоторый тепловой поток. В задачи диссертационной работы не входит определение температурного поля. Поэтому предполагается, что температура распределяется по длине стержня по следующему закону:
(11)
где 
– скорость роста температуры.
Таким образом, на первом этапе вычисляем распределение температурного поля по оси стержня . На следующем этапе – распределение физико-механических и релаксационных параметров по оси стержня 
в зависимости от температурного поля. На третьем – определяется напряженно-деформированное состояние полимерного стержня. Пусть стержень обладает некоторой начальной погибью
(12)
где – стрела начального погиба стержня; – длина стержня.
Если считать нагружение мгновенным, то в момент времени будут справедливы начальные условия . Таким образом, на нулевом этапе приходим к упругой задаче.
Граничные условия описываются соотношениями:
(13)
где 
– погибь исследуемого стержня; 
– углы поворота нормального к продольной оси стержня сечения.
Вводя обозначение 
и обозначив штрихом дифференцирование по 
, полученную краевую задачу можно сформулировать следующим образом:
(14)
(15)
где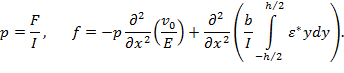 
Вводим на интервалах интегрирования равномерные сетки
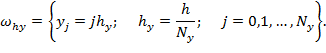
Краевым задачам можно поставить в соответствие схему четвертого порядка аппроксимации
(16)
Где
Граничные условия (13) в точках 
и 
аппроксимируются следующим образом (рис.1):
(17)
Рис. 1. Аппроксимация граничных условий задачи при варианте закрепления «защемление-защемление»
Полученную разностную схему можно представить в виде системы линейных алгебраических уравнений:
(18)
где 
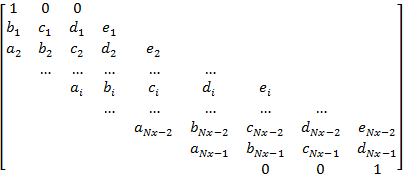
а компоненты матрицы 
и правой части 
, с учетом (17), определяются по формулам:
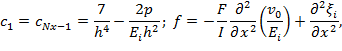
где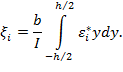 
Интеграл вычисляем с помощью метода Симпсона:
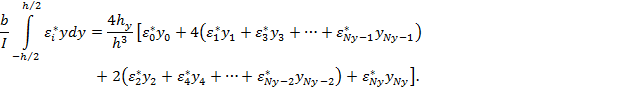(19)
Решение уравнения (18) можно получить различными методами (Гаусса, Крамера и т.д.).
Определив на нулевом этапе все необходимые величины (температурное поле, значения физико-механических и релаксационных параметров полимера, деформации, напряжения), можно найти скорость деформации ползучести 
Предполагая, что шаг по времени 
может быть сколь угодно малым, можно осуществить линейную аппроксимацию по времени и вычислить деформации ползучести на следующем «временном слое»
:
Литература:
1. Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1975. – 984 с.
2. Андреев В.И. Некоторые задачи и методы механики неоднородных тел: Монография – М.: Издательство АСВ, 2002. – 288 стр.