Численное моделирование динамических систем с большим числом степеней свободы на импульсные воздействия
Аннотация
В статье рассматривается задача численного моделирования динамических систем с большим числом степеней свободы на импульсные воздействия. Затронуты вопросы актуальности и значимости численного моделирования на сегодняшний день с учетом масштабности современных задач исследования.
Ключевые слова: численное моделирование, динамические системы, импульсные нагрузки
Для реализации каких-либо натурных экспериментов в рамках научного исследования необходимы порой большие затраты как физические, так и экономические. Чтобы поставить опыт на какие-либо динамические испытания необходимо дополнительное оборудование, в зависимости от поставленной задачи, анализ полученных экспериментальных данных и пр.
В свою очередь, для получения определенных результатов большую роль играет сложность постановки эксперимента. Не всегда удается выполнить те, или иные задачи в рамках натурного эксперимента для достижения необходимого результата. Особенно это отражено в динамической постановке задачи. Если эксперименты, к примеру, связанны с гидро и аэродинамикой, то реализовать подобный эксперимент очень сложно – не всегда жидкость, или газ в определенном пространстве ведет себя одинаково, следовательно порой трудно определить результат, который получится в ходе подобного эксперимента. Это касается и динамических экспериментов разрушающего характера, связанных с большими рисками как для используемой аппаратуры и оборудования, так и для человека, находящегося поблизости.
Поэтому в данных случаях целесообразно применять численные эксперименты. При численных расчетах вероятность получения точного и с малой долей погрешности результата возрастает. Преимущество так же в том, что количество экспериментов не ограниченно, и временные рамки гораздо шире.
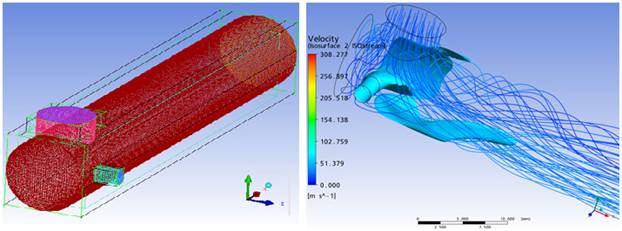
Рис.1. Применение программного комплекса Ansys для расчета гидродинамического смесителя
Благодаря прогрессу технологии ушли далеко вперед. На сегодняшний день основная часть деятельности человека компьютеризирована. В научной сфере это позволило создавать программные комплексы, решающие любые задачи различной степени сложности. Данные программы ориентированы на разные сферы научного интереса как в гуманитарных отраслях – экономике, медицине, криминалистике, так и в технических – космических, строительных, и др. Особенно это касается расчетных направлений.
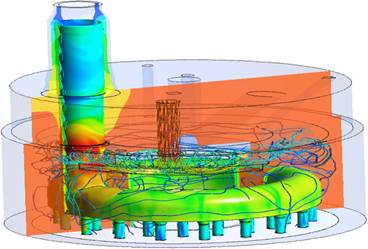
Рис.2. Результаты расчетов температурного состояния теплообменника
В строительной сфере есть свои подразделы. Например программный комплекс ЛИРА включает в себя : ЛИР-АРМ – конструирующую систему армирования, ЛИР-СТК – стальные конструкции, ЛИР-КС – конструктор сечений и пр., что предполагает его широкое применение. Во все расчетные программы, такие как Лира, Ansys, MicroFE в основном, заложены численные методы. По результатам расчета, пользователь может получить плоскостное, или пространственное изображение рассматриваемого объекта. Современные программные комплексы позволяют так же задействовать численное моделирование. Таким образом, результат можно получить в виде анимационной графики где может быть представлен результат, или сам эксперимент в течение определенного заданного промежутка времени. Ниже приведен пример моделирования процесса прогрессирующего разрушения конструкции при сейсмических и аварийных воздействиях в нелинейной динамической постановке.
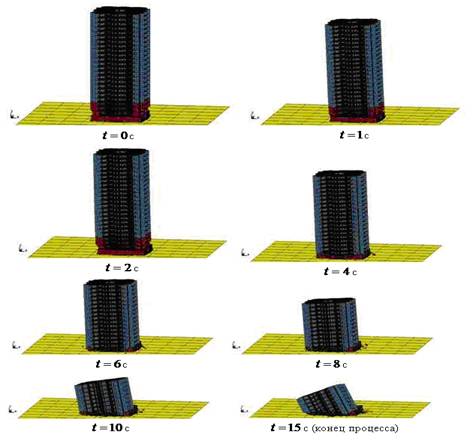
Рис.3. Процесс разрушения здания во времени
Численные эксперименты очень упрощают и гарантируют определенную степень безопасности при проведении некоторых экспериментов. В свою очередь – минимальные трудовые затраты и экономические ресурсы.
При рассмотрении импульсных задач, возникают свои сложности. При изучении ударных, взрывных и пр. нагрузок от естественных, или искусственных очагов того или иного происшествия принято заменять их на импульсные воздействия (нагрузки). Динамические эффекты в рассматриваемом объекте от подобных воздействий имеют приближенно одинаковую структуру. Основным результатом является график импульсного колебания с учетом коэффициента демпфирования.
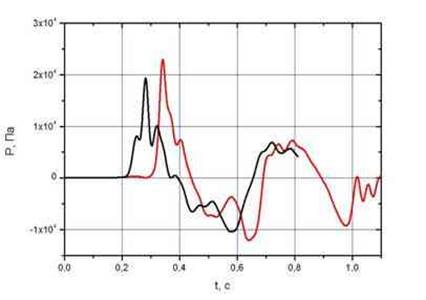
Рис.4. Избыточное давление на фасад здания для двух режимов детонации.
Поэтому при изучении данных воздействий в численной постановке рассматривается одна и та же задача с импульсной нагрузкой. Иными являются лишь исходные данные – сила и мощность удара, радиус (обширность) очага, и др. параметры. Численное моделирование подобных задач позволяет охватить широкий спектр возможных вариантов событий, так же сократить временные рамки – быстрее и точнее получить необходимый результат. Здесь же преимущество в том, что на реальных экспериментальных площадках порой нет возможности поставить эксперимент, например, на взрывоустойчивость всей конструкции, а не только ее части, и т.д.
В ходе исследования подобных импульсных нагрузок число экспериментальных данным с каждым разом возрастает в зависимости от масштабности задачи. Так же возникает временной фактор исследуемых событий. Взрывы и ударные воздействия занимают всего доли секунд, поэтому для получения всей картины масштабности исследуемого процесса необходим очень маленький шаг по временной шкале. Современные программные комплексы позволяют рассматривать подобные системы с большим числом степеней свободы, однако ресурсы ЭВМ порой затягивают временные рамки получения результата. Поэтому при расчете подобных систем с большим числом степеней свободы для снижения потребности во времени можно учитывать схему прямого явного интегрирования:
![]()
Вручную подобные расчеты сложно вести. Современные программные продукты, в основе которых лежит численное моделирование позволяют рассмотреть динамические системы с большим числом степеней свободы и получить наглядный результат. Однако для экономии времени и получения более точных данных на меньшей временной шкале можно вносить изменения в расчетный процесс на примере дополнительных модулей.
Литература:
1.Мкртычев О.В., Мкртычев А.Э.Расчет большепролетных и высотных сооружений на устойчивость к прогрессирующему обрушению при сейсмических и аварийных воздействиях в нелинейной динамической постановке / ЦНИИСК, МГСУ.
2.LS-DYNA. Воздействие взрыва на здания и сооружения http://www.cae-services.ru/
3.Марчук Г.И / Методы вычислительной математики. / М.: Наука.1980.