Использование непрерывного вейвлет преобразования для анализа токового сигнала при диагностировании дефектов в червячной передаче

П.В. Синельщиков; А.В.Чернов

Использование непрерывного вейвлет преобразования для анализа токового сигнала при диагностировании дефектов в червячной передаче

Аннотация

П.В. Синельщиков, А.В.Чернов

Приводится экспериментальное исследование частотных составляющих токовых сигналов, снятых с электродвигателя экспериментальной установки с внесенным дефектом в червячную передачу. Указываются ограничения Фурье – преобразования, которые не позволяют точно определить место дефекта. Приводятся результаты анализа токового сигнала при помощи непрерывного вейвлет - преобразования.
Ключевые слова: диагностика,электроприводное оборудование, вейвлет - преобразование, Фурье – преобразование.

05.13.18 - Математическое моделирование, численные методы и комплексы программ

На сегодняшний день широкое распространение получили методы диагностирования электромеханического оборудования с использованием токового сигнала, который регистрируется со статорных обмоток электродвигателя при работе привода. Мобильность данного подхода и относительная оперативность, выдаваемых им результатов контроля позволяют производить измерения дистанционно, вдали от исследуемого оборудования, когда доступ к объекту контроля затруднен или невозможен, например, ввиду наличия высокой температуры.
Спектральный анализ сигналов - наиболее распространённый способ анализа сигналов. В подавляющем большинстве случаев используется преобразование Фурье (или его развитие - оконное преобразование Фурье) для получения спектра частот сигнала [1, 2]. Следует отметить, что практическое применение методов спектрального анализа с использованием преобразования Фурье не эффективно для нестационарных сигналов. Данные трудности могут быть преодолены за счет использования свойства локальности непрерывного вейвлет-преобразования, что позволяет анализировать и обрабатывать нестационарные (во времени) или неоднородные (в пространстве) сигналы [3, 4].
В статье [5] показано, что при помощи непрерывного вейвлет - преобразования (НВП) можно производить анализ частотных составляющих токового сигнала. Так же в ней указывается, каким образом может быть использовано НВП при ограничениях накладываемых дискретностью токового сигнала.
Экспериментальная оценка метода диагностирования с использованием НВП была выполнена на испытательной установке, показанной на рис. 1.

стенд

Рис.1 Испытательная установка

Установка представляет собой станину, на которой смонтированы червячный редуктор, электромагнитный тормоз (ЭТ), приводной электродвигатель и пульт управления.
Эксперимент состоял в последовательном увеличении зазора между зубом червячного колеса и витками червяка. Это достигалось путем

уменьшения толщины зуба червячного колеса посредством его периодического механического стачивания. Для каждого опыта производилась запись токового сигнала при различных вариантах нагрузок создаваемых ЭТ: отсутствие, половина максимальной, максимальная.

Рис.2 Внешний вид червячного колеса

Рис.3 Внешний вид подпиленной контактной поверхности зуба червячного колеса

Рассмотрим пример использования предлагаемой методики определения технического состояния для опыта, при создаваемой ЭТ максимальной нагрузке, когда толщина зуба червячного колеса была уменьшена на 1,2 мм и составила 3,6мм. Токовый сигнал, записанный для этого опыта, показан на рисунке 4.

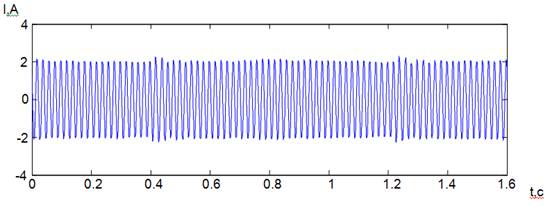
Рис. 4 Токовый сигнал

Как видно из рисунка, с периодичностью равной одному обороту червячного колеса, в токовом сигнале появляются возмущения. То есть, в результате уменьшения толщины зуба червячного колеса и деградации червячной пары, вместо процессов трения при скольжении витка червяка по зубу червячного колеса, стали происходить динамические удары (входа и выхода из зацепления дефектного зуба).
Воспользовавшись записанным токовым сигналом, построим его Фурье – спектр (рис. 5) и вейвлет - спектр (рис. 6).

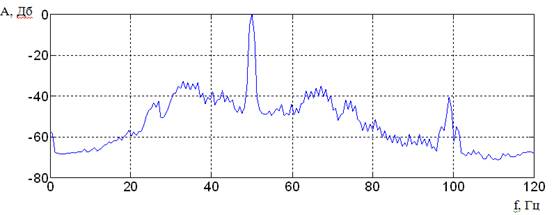
Рис. 5 Фурье – спектр токового сигнала

В результате появления данного дефекта, в спектре, построенном при помощи преобразования - Фурье (рис. 5), происходит «размытие» частотных составляющих и сделать однозначный вывод о виде дефекта не представляется возможным.
По записанному токовому сигналу (рис. 4), после удаления сетевой составляющей, построен его вейвлет - спектр (рис. 6). В полученном вейвлет - спектре обнаружены характерные участки, один из которых отображен на рисунке 7.

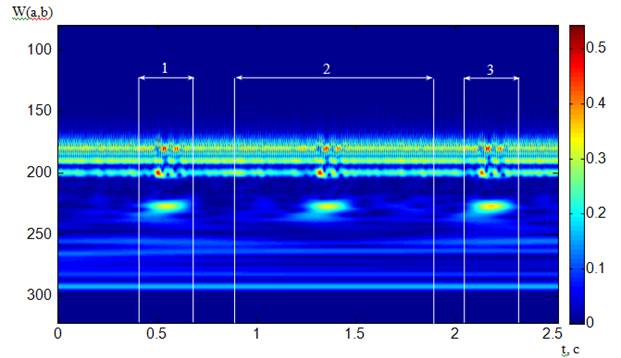
Рис.6 Вейвлет - спектр на интервале 2.5 секунд

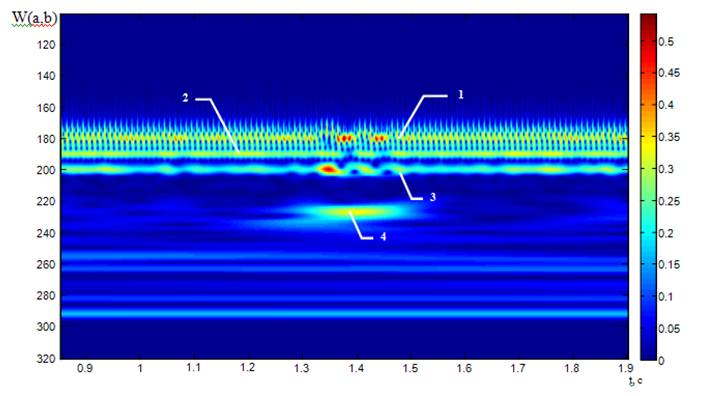
Рис.7 Вейвлет - спектр участка от 0.85 до 1.9 секунд

В полосе 1 вейвлет коэффициентов (рис. 7), наблюдаются нестационарности (в интервале от 1,3 до 1,5 секунд), в связи с изменением условия контакта поверхности зуба червячного колеса и червяка. Цифрами 2,3 – отмечены полосы частот отражающие процессы взаимодействия деталей в подшипниках, 4 – колебание появившиеся в результате удара.
С помощью НВП можно производить мониторинг изменения частотных составляющих, путем анализа восстановленного сигнала по определенной полосе вейвлет коэффициентов.
В результате проведенных экспериментов в токовом сигнале однозначно определены частоты, характерные для дефекта зуба червячной передачи. С помощью непрерывного вейвлет - преобразования появилась возможность не только контролировать амплитуду частотных составляющих токового сигнала, но и так же осуществлять мониторинг их изменения. Применение метода на практике подтвердило его хорошую чувствительность к определению дефектов при наличии нестационарностей, возникающих при дефектах элементов электромеханического оборудования.

Использование непрерывного вейвлет преобразования для анализа токового сигнала при диагностировании дефектов в червячной передаче

Литература: