Центробежное фракционирование соломистой массы

Аннотация

М.Н. Московский, А.В. Погорелов, А.А. Бойко, А.П. Марков, А.А. Гуляев

В данной  работе рассматривалось фракционирование соломистого вороха при  получении соломистой подстилки. Был предложен  принцип центробежного фракционирования соломистой массы и определены основные процессы разделения соломистой массы. Был произведен математический анализ данного процесса.Результаты моделирования разброса частиц свидетельствуют о принципиальной возможности реализации процесса фракционирования частиц соломистой массы центробежным рабочим органом сепарирования.
Ключевые слова: Соломистый  ворох, воздушный поток, центробежное фракционирование, математическое моделирование, закон распределения, вероятность распределения.

Широкое распространение получила технология с использованием глубокой подстилки при напольном выращивание бройлеров. Материалом для подстилки служат древесные опилки, стружка, лузга семян подсолнечника, измельчённые стержни початков кукурузы торф и др. Перспективным материалом для подстилки являются соломистые материалы. Однако солома, прошедшая простое измельчение, не соответствует зоотехническим требованиям: содержит патогенную микрофлору и неоднородность по длине резки. Рекомендованная  длина резки должна составлять от 100 мм, до 180 мм. Тем самым возникает задача фракционирования соломистой массы, получаемой при уборке зерновых культур в качестве отходов.
Разработан экономически обоснованный технологический процесс подготовки соломистой подстилки из отходов комбайновой уборки зерновых включающий обеззараживание, измельчение ножевым барабаном и фракционирование продуктов измельчения [1].
Для фракционирования соломистой массы предлагается использовать центробежный сепарирующий рабочий орган. Принцип центробежного фракционирования основан на аэродинамической сепарации потока частиц, разбрасываемого быстровращающимся диском.
Нами была установлена расчетная схема процесса центробежного фракционирования. При обосновании расчётной схемы сделан ряд допущений, упрощающих решение задачи [2]. Расчётная схема (рис. 1) представляет плоский диск, вращающийся на вертикальном валу с угловой скоростью ω. По диску под действием центробежной силы движется шероховатая соломистая частица с коэффициентом трения  о диск f . Частица сбрасывается с диска со скоростью V_o и проходит в воздушном зазоре между обечайкой и диском, подвергаясь воздействию воздушного потока со скоростью u. Так как частицы имеют разную массу, форму и парусность, то траектории их в воздушном потоке будут разные. Лёгкие и оболочечные частицы будут выдуваться наверх, тяжёлые, длинные падать вниз по разным траекториям. Разделение на фракции осуществляется кольцевыми каналами, расположенными  на пути потока сброшенных с диска частиц.

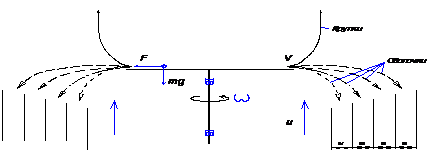
Рис. 1. Расчётная схема центробежного фракционирования.

В расчётной схеме присутствуют три разных процесса: процесс движения соломистой шероховатой частицы по вращающемуся диску назовём процессом разгона; процесс движения частицы в воздушном потоке в кольцевом зазоре с начальной скоростью ; процесс сортировки по частиц по кольцевым каналам.
Соответственно математическая модель  включает модели трёх процессов.

рис. 2.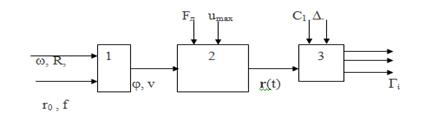

Рис. 2. Структурная схема модели центробежного фракционирования: m- масса частицы, ω- скорость вращения диска, r₀ -координаты попадания частицы на диск, R - радиус диска, f- коэффициент трения частицы о диск;  v- скорость частицы при сходе с диска φ- направление;V_в - воздушного потока со скоростью; V_с - скорость частицы при сходе с диска; F_л -сила лобового сопротивления; u_max- скорость витания r(t)-траектория движения частицы в аэродинамическом канале; С₁С₂С₃- радиусы сепарирующих цилиндров; Δ₁, Δ₂, Δ₃- ширина кольцевых зазоров; Δ -ширина аэродинамического канала.

Нами были рассмотрены  все три процесса, и был произведен их математический анализ.
Математическое моделирование движение частицы по диску.  Рассмотрим движение частицы массой m по горизонтальному диску с прямыми лопастями, установленными под углом Ψ к радиусу (рис.3).

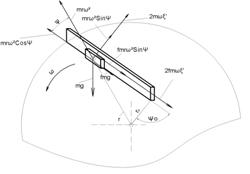
Рис. 3. Схема сил, действующая на частицу
при движении по диску с прямыми лопастями

Скорость относительного движения частицы вдоль направления лопасти :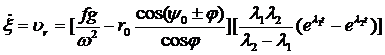
        (1)
Учитывая, что переносная скорость представлена окружной скоростью v_e=rω, то, проектируя относительную скорость v_rна касательную к окружности периферии диска, найдем скорость рассева частиц в этом направлении как алгебраическую сумму этих скоростей:
,    (2)
где ψ₁ — конечное значение угла ψ.
Следовательно, угловое перемещение частицы в абсолютном движении будет:
    (3)
здесь знак минус — для лопасти, наклоненной назад, и плюс — для лопасти,   наклоненной   вперед.
На основе полученных уравнений можно рассчитать и выбрать рациональные конструктивные параметры и режимы их работы аппаратов дляразгона частицы на вращающемся диске.
Моделирование процессов разбрасывания. Нами получена развёрнутая математическая модель процесса в виде системы нелинейных дифференциальных уравнений второго порядка:
        (4)
      (5)
Аналитически эти уравнения не решаемы.
Для построения траекторий относительного движения частиц, полученные уравнения уравнения решали методом компьютерного имитационного моделирования в среде Simulink MatLab.
По разработанной модели рассчитаны скорости и траектории частиц  соломистой массы. На рис. 4представлены траектории абсолютного движенияy(x) частиц в равномерном воздушном потоке при режиме сепарации: и = 32м/с, w = 1,52м/с, β = 30°, α=320°, u_{вит.тяжел} = 15-45 м/с, u_{вит.лёгк} = 4-10 м/с.
Результаты моделирования говорят о большой разнице в траекториях частиц лёгкой и тяжёлой фракций. В центробежном поле траектории частиц различной массы и размеров отличаются так сильно, что можно говорить о сепарационных свойствах сочетания центробежного поля сил и воздушного потока.

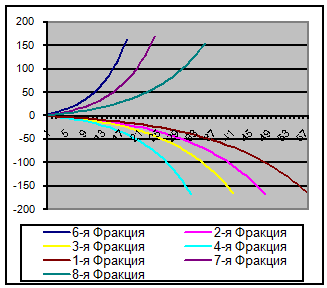
Рис. 4. Траектории движения частиц в воздушном потоке при центробежной сепарации.

Моделирование процесса разделения на фракции.
Показателем различия частиц считаем величину толщины потока. Величина толщины потока С1…С4 равна  расстоянию между точками пересечения крайних траекторий с наклонными прямыми, проводимыми из следа оси диска с уровнем пола и определялась как по формуле:
   ,    (6)
где (х₁, у₁) и (х₂, у₂) – координаты точек пересечения крайних траекторий с наклонными прямыми.
Угол наклона рекомендуется принимать 30 градусов.
Тогда  задача максимизации сепарационных свойств, конкретизируется так: найти такое значение параметров модели, которое обеспечит максимальное значение толщины слоя нижнего потока во всём диапазоне изменения обобщённого квалификационного признака К_Р.
Изменяя классификационный показатель К_Р от минимального значения  до максимального получаем нужные толщины потока.
Проведённые расчёты по структурным моделям в среде Simulink показали, что при изменении классификационного показателя К_Р от 100 до 20000 длина зоны С₁-С₄ составляет 2500 мм.
Это означает, что устанавливая разделительные перегородки через 500 мм, можно просто получать необходимое разделение на 5 фракций, что вполне приемлемо для практики.
Выводы. Математическая модель центробежного фракционирования состоит из трёх моделей процессов: модель разгона частиц по центробежному диску, описываемая дифференциальными  уравнениями (1) и (3); модель движения частицы в потоке воздуха под действием воздушного потока в зазоре между обечайкой и диском, описываемая нелинейными дифференциальными уравнениями (4) и (5); модель процесса разделения разлетающихся частиц по фракциям между сепарирующими цилиндрами, описываемая сечением траекторий наклонной плоскостью. С1, Δ₂, Δ₃.
Результаты моделирования разброса частиц свидетельствуют о принципиальной возможности реализации процесса фракционирования частиц соломистой массы центробежным рабочим органом сепарировании.

Список использованных источников:

1.Московский М.Н., Погорелов А.В. Анализ экономической эффективности использования соломистой подстилки при технологии напольного содержания  птицы в  ПТФ / Естественные и технические науки №6(47), Москва , 2010. с. 417-420
2.Теория, конструкция и расчёт сельскохозяйственных машин/ Е.С. Босой и др. / Под ред Е.С. Босого. - М.: Машиностроение, 1977. – 568 с.