Аналитическое определение формы образующей конического бункера наибольшей пропускной способности сыпучих материалов

Аннотация

Ляшенко А.С

Дата поступления статьи: 15.06.2014

В статье приводится аналитическое решение по определению образующей стенки бункера наибольшей пропускной способности среди всех бункеров имеющих одинаковые входные и выходные отверстия. Такие бункеры предназначены для гидравлического вида истечения сыпучего материала. Они снижают пульсацию сыпучего при его выходе из выпускного отверстия и уменьшают степень влияния динамических сводов на расходные характеристики бункера.

Ключевые слова: бункер, сыпучее тело, линии скольжения, входные отверстия, выпускные отверстия, расход сыпучего.

Для решения этой задачи примем прямой усечённый конус (рис.1).

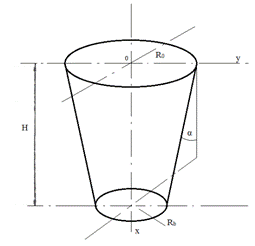
Рис. 1. - Конический бункер

Обусловлено это широким их использованием в производстве из-за простоты конструкции и относительно небольших материальных затрат на их изготовление [1].
Такие бункеры устанавливаются, например, на разбрасывателях минеральных гранулированных удобрений (МВУ-0.5), дозирующих устройствах, кормоцехах, хранилищах зерна и т.д. и т.п.
Как известно, в любом поперечном сечении этого бункера скорость сыпучего тела определяется по формуле

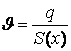,                                                       (1)

где q - объёмный расход сыпучего, м3/с;
S(x) - площадь текущего поперечного сечения бункера, м2.
Тогда, ускорение сыпучего в этом поперечном сечении бункера

.                                               (2)

Выполнив дифференцирование и положив a=g, найдём соотношение между объёмным расходом и объёмным ускорением сыпучего тела (дифференциальное уравнение истечения) в случае, если рассматриваемое сечение xбудет служить выпускным отверстием бункера
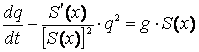.                                       (3)
Решение этого дифференциального уравнения имеет вид
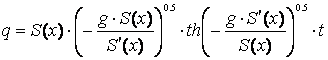                   (4)
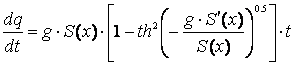.                 (5)
Если в формуле (3) положить  , или в формулах (4) и (5) устремить t→∞, получим предельный расход бункера при условии, что рассматриваемое сечение xявляется выпускным отверстием бункера
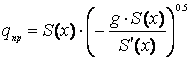.                                       (6)
У усечённого конусного бункера площадь поперечного сечения равна
,                                                (7)
а формула для предельного расхода сыпучего получает вид
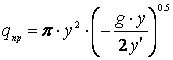.                                   (8)
Пользуясь формулами (7) и (8), можно построить кривую зависимости предельного расхода от абсциссы xпоперечного сечения для бункера с любым криволинейным продольным его сечением.
Истинный предельный расход бункера будет, очевидно, определяться сечением, которое имеет наименьшую пропускную способность [2 - 4]. В случае конического бункера, который является сужающимся, таким сечением будет являться выпускное отверстие, так как оно имеет наименьшие размеры, величина же  Зависимость q_пр=f(x) у такого бункера монотонно убывает.
Для бункера с криволинейным продольным сечением зависимость qпр=f(x) может иметь в интервале 0<x<Hминимумы. Сечение xmin, соответствующее наименьшему минимуму функцииq_пр=f(x) , ограничивает пропускную способность (расход сыпучего) всего бункера. Струя сыпучего материала претерпевает в этом случае разрыв, так как при x>x_min частицы дискретного сыпучего тела совершают свободное падение с ускорением g[5].
Таким образом, для определения истинного расхода сыпучего дискретного материала из бункера с кривой его образующей достаточно найти наименьший минимум функции (6) или наименьшее значение этой функции в интервале 0<x<H. При исследовании, при этом, удобнее рассматривать функцию
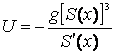.                                                  (9)
Для сыпучего тела нетрудно решить и другую важную задачу - найти форму кривой продольного сечения, обеспечивающую наибольшую пропускную способность бункера. В этих случаях необходимо добиться того, чтобы максимальный расход каждого последующего (более узкого) сечения был не меньше максимального расхода предыдущего сечения [6]. В пределе - расход каждого последующего сечения должен быть равен расходу предыдущего (бункер постоянной во всех сечениях пропускной способности).
Бункер, форма которого определена из указанного условия, имеет наибольшую пропускную способность среди всех бункеров, имеющих заданные параметры входного отверстия, и может быть назван бункером наибольшего расхода [7].
Приравняв нулю производную выражения (9), получим дифференциальное уравнение, определяющее поверхность бункера наибольшего предельного расхода:
.                                           (10)
Проинтегрируем уравнение (10), приняв начальные условия S(0)=S0; S'(0)=S'0 .
Получим следующее соотношение между площадями и абсциссами поперечных сечений бункера наибольшего расхода:
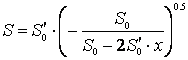.                                      (11)
Предельный расход такого бункера, согласно формуле (6), определяется параметрами   и  входного отверстия
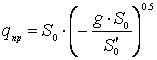.                                    (12)
Решив формулу (11) относительно  и подставив   в уравнение (12), получим зависимость между S и xпри заданном предельном расходе бункера и площади начального его сечения:
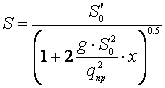.                                          (13)
В частности, если положить y(0)=R0; y'(0)=-b0=-tgα, то формулы (11), (12), (13) для решаемого бункера примут вид (рис. 2).
;                                          (14)
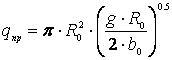.                                        (15)
Этот бункер предназначен для гидравлического вида истечения сыпучего материала, при котором движение последнего ламинарное, без заметных пульсаций.

Гидравлическое истечение сыпучего происходит, как указывается в работе Л.В. Гячева [8], при условии 0≤α0<90о-(β+Ψ+φпр), где β - угол укладки частиц в бункере; Ψ - угол трения между частицами; φпр - приведённый угол трения потока частиц о граничную поверхность бункера.

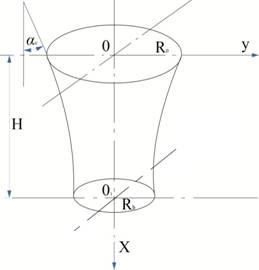
Как следует из опыта эксплуатации бункеров, их продольное сечение стремятся выполнить по продольному сечению потока «рис.3», наблюдаемому при нормальном его истечении. При этом истечении его продольная образующая фактически описывается установленными зависимостями (14) и (15).

Рис. 3. - Нормальный вид истечения сыпучего тела из бункера
(овес)

Объясняется это тем, что граничные линии скольжения такой формы «рис.3» являются линиями скольжения наименьшего сопротивления сдвигу [9, 10] дискретного сыпучего тела, что обуславливает его равномерный выход из выпускного отверстия бункера, то есть, равномерное распределение дискретных частиц сыпучего по его площади.
Таким образом конические бункеры с образующей их стен, выполненной по формуле (14), являются бункерами наибольшей пропускной способности зернистых сыпучих материалов.

Литература

1. Вельшоф Г. Определение расхода сыпучих материалов // Сельское хозяйство за рубежом. 1962. №4. С. 67-69.
2. Попов А.Ю., Казачков И.А. К теории дозирования семян пневматическим высевающим аппаратом избыточного давления // Инженерный вестник Дона, 2014, №2 URL: ivdon.ru/ru/magazine/archive/n2y2014/2345/.
3. Richmond O. Gravity hopper design. Mechanical Engineering. 1963. №1. pp. 254-261
4. Скурятин Н.Ф., Мерецкий С.В. Совершенствование процесса посева зерновых на склоновых почвах // Инженерный вестник Дона, 2012, №1 URL: ivdon.ru/magazine/archive/n1y2012/662/.
5. Банит Е.А. Исследование процесса истечения сыпучих материалов из отверстия сосудов: дис. ... канд. техн. наук: 05.20.01. Одесса, 1959. 157 с.
6. Баранова А.Б. Исследование влияния сводообразования на истечение сыпучих материалов: дис. ... канд. техн. наук: 05.20.01. Ростов-на-Дону, 1973. 107 с.
7. Битюков В.А. Исследование механики движения сыпучих материалов в аппаратах: дис. ... канд. техн. наук: 05.20.01. М., 1967. 155 с.
8. Гячев Л.В. Основы теории бункеров. Новосибирск: Новосибирский университет, 1992. 310 с.
9. Богомягких В.А. Пепчук А.П. Интенсификация разгрузки бункерных устройств в условиях сводообразования зернистых материалов // ВНИПТИМЭСХ. 1995. С. 164.
10. Jenike A.W. Gravity flow of solids. Trans. of the institution of chemical Engineering. 1962. № 5. pp. 264-274.

References

1. Vel'shof G. Sel'skoe khozyaystvo za rubezhom. 1962. №4. pp. 67-69.
2. Popov A.Yu., Kazachkov I.A. Inženernyj vestnik Dona (Rus), 2014, №2 URL: ivdon.ru/ru/magazine/archive/n2y2014/2345/.
3. Richmond O. Gravity hopper design. Mechanical Engineering. 1963. №1.
4. Skuryatin N.F., Meretskiy S.V. Inženernyj vestnik Dona (Rus), 2012, №1. URL: ivdon.ru/magazine/archive/n1y2012/662/.
5. Banit E.A. Issledovanie protsessa istecheniya sypuchikh materialov iz otverstiya sosudov: dis. ... kand. tekhn. nauk: 05.20.01. Odessa, 1959. 157 p.
6. Baranova A.B. Issledovanie vliyaniya svodoobrazovaniya na istechenie sypuchikh materialov: dis. ... kand. tekhn. nauk: 05.20.01. Rostov-na-Donu, 1973. 107 p.
7. Bityukov V.A. Issledovanie mekhaniki dvizheniya sypuchikh materialov v apparatakh: dis. ... kand. tekhn. nauk: 05.20.01. M., 1967. 155 p.
8. Gyachev L.V. Osnovy teorii bunkerov. Novosibirsk: Novosibirskiy universitet, 1992. 310 p.
9. Bogomyagkikh V.A. Pepchuk A.P. Intensifikatsiya razgruzki bunkernykh ustroystv v usloviyakh svodoobrazovaniya zernistykh materialov. VNIPTIMESKh. 1995. p. 164.
10. Jenike A.W. Gravity flow of solids. Trans. of the institution of chemical Engineering. 1962. № 5. pp. 264-274.