Математическая модель деформирования ортотропных конических оболочек

Аннотация

А.А. Семенов, А.А. Овчаров

Дата поступления статьи: 28.05.2014

В статье приводится математическая модель деформирования тонкостенных конических оболочек, с учетом ортотропии материала, геометрической нелинейности и поперечных сдвигов. Показаны геометрические соотношения, физические соотношения, функционал полной энергии деформации и краевые условия.

Ключевые слова: конические оболочки, конические панели, математическая модель, геометрическая нелинейность, ортотропия, поперечные сдвиги

05.13.18 - Математическое моделирование, численные методы и комплексы программ

05.23.17 - Строительная механика

Введение

Наиболее широкое применение конические оболочки находят в авиационной технике и машиностроении. Одной из первых работ по исследованию устойчивости конических оболочек была работа Х.М. Муштари [1]. Также здесь необходимо отметить вклад Н. А. Алумяэ, Э. И. Григолюка, А. В. Саченкова [2] и др. В работе Н. В. Валишвили [3] исследуется устойчивость конических оболочек на основе осесимметричной теории. В работе [4] задача устойчивости конических оболочек была сведена к отысканию собственных значений системы дифференциальных уравнений в частных производных с переменными коэффициентами, и было показано, что решение необходимо искать приближенно.
Одним из применяемых ранее подходов к решению данной проблемы было сведение конической оболочки к цилиндрической. Радиус цилиндрической оболочки принимался как среднее между большим и малым радиусами конической оболочки. Данная методика хорошо себя показала при расчете оболочек с малым углом конусности [5], но при его увеличении специфичность строения конической оболочки начинает сильнее сказываться на ее устойчивости, и такой подход становится неприемлемым.
По сравнению с расчетом цилиндрических оболочек, исследовать такие конструкции труднее. Это проявляется, прежде всего, в усложнении геометрических соотношений, связывающих перемещения и деформации. К недавним работам в области исследования конических панелей и оболочек следует отнести статью F. Shadmehri, S.V. Hoa и M. Hojjati [6], в которой рассматриваются замкнутые конические оболочки из композиционных материалов, но математическая модель строится на теории первого порядка, а также не учитывается геометрическая нелинейность.
В работах [7, 8] были получены уравнения движения для подкрепленных ребрами жесткости конических оболочек при линейно-упругом деформировании с учетом поперечных сдвигов.
В исследовании [9] показана математическая модель деформирования оболочки, но не учитываются поперечные сдвиги и ортотропия материала.
В работе [10] приводится математическая модель деформирования оболочки на основе функционала полной энергии деформации, которая учитывает геометрическую и физическую нелинейности, поперечные сдвиги, возможность развития деформации ползучести, введение ребер жесткости с помощью метода конструктивной анизотропии с учетом сдвиговой и крутильной жесткости, но без учета ортотропии материала.
Математическая модель деформирования подкрепленных ортотропных оболочек общего вида на основе функционала полной энергии деформации была представлена в работе [11].
Цель исследования
Целью данной работы является построение математической модели деформирования конических оболочечных конструкций на основе функционала полной энергии деформации с учетом ортотропии материала, геометрической нелинейности и поперечных сдвигов.
Материал и методы исследования
Схематичное изображение панели конической оболочки показано на Рисунке 1.
Математическая модель деформирования оболочки строится на основе функционала полной энергии деформации (или уравнений равновесия), а также включает в себя геометрические соотношения, физические соотношения и граничные условия.

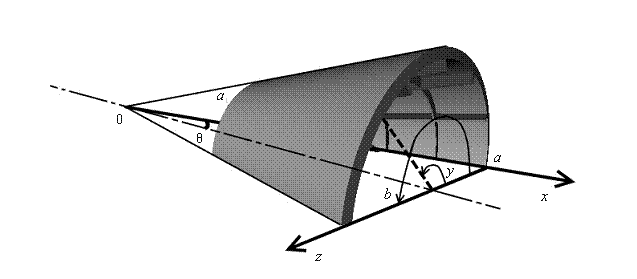
Рис. 1. – Схематичное изображение и принятая локальная система координат панели конической оболочки

Модель Кирхгофа-Лява, когда неизвестными являются только три функции перемещений  и в уравнениях равновесия функции  и  имеют вторые производные, а функция  – четвертые, дает существенную погрешность. Необходимо учитывать еще и поперечные сдвиги, т.е. рассматривать модель Тимошенко-Рейснера. Тогда неизвестными будут пять функций – три функции перемещений точек координатной поверхности  и две функции, характеризующие углы  поворота нормали в плоскостях : . При этом получаемая модель будет геометрически нелинейной, т.е. зависимость деформаций от перемещений – нелинейная, что позволяет исследовать не только напряженно-деформированное состояние оболочки, но и ее устойчивость. В дальнейшем будем рассматривать только модель Тимошенко-Рейснера.
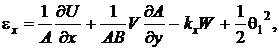
В рассматриваемой модели геометрические соотношения для срединной поверхности оболочки принимают вид [1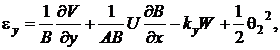1]

          (1)                                            


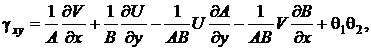
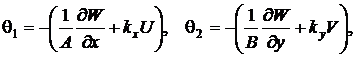
где  – деформации удлинения вдоль координат ,  срединной поверхности;  – деформации сдвига в плоскости ; ,, – параметры Ляме, характеризующие геометрию оболочки и главные кривизны оболочки вдоль осей  и . Для конической оболочки они принимают вид   и  . Из-за наличия в формулах  зависимости от координаты , сложность системы соотношений (1) существенно возрастает.
Функции изменения кривизн , и кручения принимают вид:

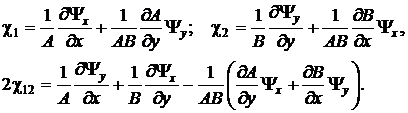
Для связи деформаций и напряжений используются физические соотношения, которые строятся на основе обобщенного закона Гука. Выразив напряжения через деформации, получим физические соотношения для тонкостенной ортотропной оболочки при линейно-упругом деформировании:

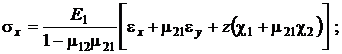
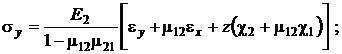    (2)                                     


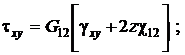
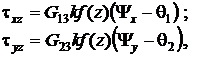
здесь  – модули упругости в направлениях , ;  – модули сдвига в плоскостях  соответственно;  – коэффициенты Пуассона;  – функция, характеризующая распределение напряжений  по толщине оболочки,  – числовой коэффициент, соответствующий выбранной функции . Для гладких оболочек принимается

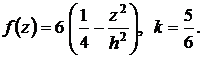
Функция  при  и  (верхняя и нижняя поверхности оболочки) обращается в нуль, а также удовлетворяет условиям [12]:
 
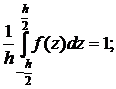
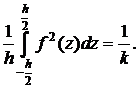
На основе физических соотношений можно сформировать выражения для усилий и моментов. Интегрируя напряжения (2) по  в пределах от  до , получим усилия и моменты, приведенные к срединной поверхности оболочки и приходящиеся на единицу длины сечения. Для гладких оболочек они будут иметь вид



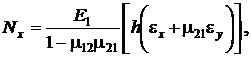
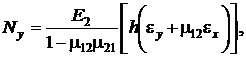
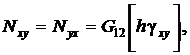
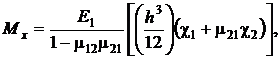     (3)                                                 




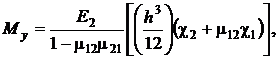
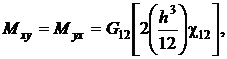
где  – нормальные усилия вдоль осей  и сдвиговые усилия в плоскости  соответственно;  – изгибающие моменты в направлении осей  и крутящие моменты;  – поперечные силы в плоскостях  и .
Функционал Лагранжа полной энергии деформации оболочки является суммой работ внутренних и внешних сил, и принимает следующий вид [11]:
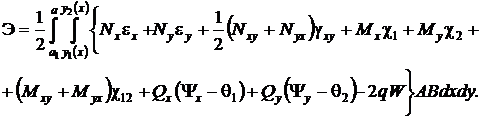(4)             
Подставив выражения для усилий и моментов (3) в функционал (4), получим



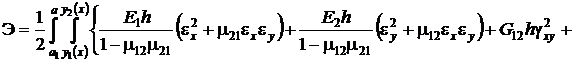
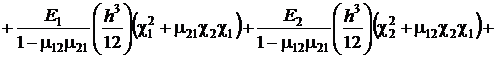
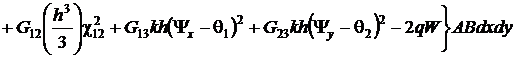
Приведя подобные члены, получим

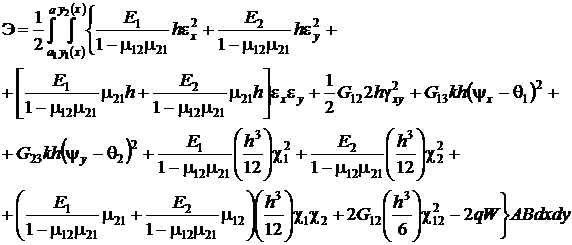
Учитывая, что , введем обозначения:

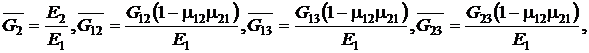
и приведем функционал к виду
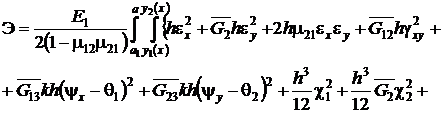 (5)                   

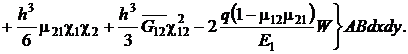
Способ закрепления контура конструкции учитывается через граничные условия (Таблица 1), которые влияют в дальнейшем на выбор аппроксимирующих функций [13], а область, занимаемая оболочкой, задается в пределах интегрирования [14]: . Использование функций  позволяет учитывать нестандартную форму контура оболочки.
Таблица № 1
Краевые условия при различном закреплении контура конструкции

Заключение
Таким образом, полученные соотношения (1), (2), (5) вместе с краевыми условиями представляют собой математическую модель деформирования конической оболочечной конструкции с комплексным учетом таких факторов, как ортотропия материала, геометрическая нелинейность и поперечные сдвиги.
Для дальнейшего исследования прочности и устойчивости рассматриваемых конструкций к представленной модели могут применяться методы, подходы и алгоритмы, представленные в работах [14 – 17].

Литература:

1. Муштари, Х. М. Об устойчивости тонкостенных конических оболочек круглого сечения при кручении парами [Текст] / Х. М. Муштари. – В кн. Сборник научных трудов КАИ. – Казань: Издательство Казанского авиационного института, 1935. – С. 39–40.
2. Муштари, Х. М. Об устойчивости цилиндрических и конических оболочек круглого сечения при совместном действии осевого сжатия и внешнего нормального давления [Текст] / Х. М. Муштари, А. В. Саченков // Прикладная математика и механика, 1954. т. XVIII, № 6. – С. 667–674.
3. Валишвили, Н. В. Методы расчета оболочек вращения на ЭЦВМ [Текст] / Н. В. Валишвили. – М.: Машиностроение, 1976. – 278 с.
4. Вольмир, А. С. Устойчивость деформируемых систем [Текст] / А. С. Вольмир. – М.: Наука, 1967. – 984 с.
5. Преображенский, И. Н. Устойчивость и колебания конических оболочек [Текст] / И. Н. Преображенский, В. З. Грищак. – М.: Машиностроение, 1986. – 240 с.
6. Shadmehri F., Hoa S.V., Hojjati M. Buckling of conical composite shells // Composite Structures. – Vol. 94. – 2012. Pp.787–792. DOI:10.1016/j.compstruct.2011.09.016
7. Овчаров, А. А. Математическая модель конической оболочки ступенчато-переменной толщины при динамическом нагружении [Текст] / А. А. Овчаров // Математическое моделирование, численные методы и комплексы программ: Межвуз. темат. сб. тр. СПбГАСУ. – СПб., 2004. – С. 127–132.
8. Овчаров, А. А.  Компьютерные технологии исследования устойчивости панелей ребристых конических оболочек [Текст] / А. А. Овчаров // Вестник гражданских инженеров. – № 2(11). – 2007. – С. 104–111.
9. Бурцева, С. В. К расчету оболочек вариационно-энергетическим методом [Электронный ресурс] / С. В. Бурцева, Г. П. Стрельников, В. И. Авилкин // Инженерный вестник Дона. – 2012. – Т. 23, № 4, Ч. 2. – С. 1–3. Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1291 (доступ свободный)
10. Баранова, Д. А. Математическая модель деформирования подкрепленных оболочек вращения при учете различных свойств материала [Электронный ресурс] // Инженерный вестник Дона. – 2012. – Т.20, № 2. – С. 45–50. Режим доступа: http://ivdon.ru/magazine/archive/n2y2012/745 (доступ свободный)
11. Карпов, В. В. Математическая модель деформирования подкрепленных ортотропных оболочек вращения [Текст] / В. В. Карпов, А. А. Семенов // Инженерно-строительный журнал. – № 5. – 2013. С. 100–106.
12. Вольмир, А. С. Нелинейная динамика пластинок и оболочек [Текст] / А. С. Вольмир. – М.: Наука, 1972. – 432 с.
13. Карпов, В. В. Математическое моделирование, алгоритмы исследования модели, вычислительный эксперимент в теории оболочек [Текст] / В. В. Карпов. – СПб.: СПбГАСУ, 2006. – 330 с.
14. Семенов, А. А. Алгоритмы исследования прочности и устойчивости подкрепленных ортотропных оболочек [Текст] / А. А. Семенов // Строительная механика инженерных конструкций и сооружений. – № 1. – 2014. – С. 49–63.
15. Карпов, В. В. Прочность и устойчивость подкрепленных оболочек вращения: в 2 ч. Ч.2: Вычислительный эксперимент при статическом механическом воздействии [Текст] / В. В. Карпов. – М: Физматлит, 2011. – 248 с.
16. Атисков, А. Ю. Компьютерные технологии расчета оболочек [Текст] / А. Ю. Атисков, Д. А. Баранова, В. В. Карпов, Л. П. Москаленко, А. А. Семенов. – СПб.: СПбГАСУ, 2012. – 184 с.
17. Qu Y., Wu S., Chen Y., Hua H. Vibration analysis of ring-stiffened conical–cylindrical–spherical shells based on a modified variational approach // International Journal of Mechanical Sciences. – Vol.69. – 2013. Pp. 72–84. http://dx.doi.org/10.1016/j.ijmecsci.2013.01.026