Анализ эффективности применения перенумерации узлов конечно-элементной сетки применительно к методу конечных элементов на трёхмерных задачах линейной теории упругости

Аннотация

А.Р. Филатов

Дата поступления статьи: 13.05.2013

В работе проводится сравнительный анализ эффективности метода Cuthill-McKee и алгоритма сужения полосы матрицы, основанного на многоуровневой вложенной парадигме разбиения, разработанной на факультете «Компьютерных наук и инженерии» университета Миннесоты. Для краткости будем называть алгоритм Cuthill-McKee CM, а алгоритм из университета Миннесоты — NodeND (Node nested dissection). В данной статье используется модификация CM алгоритма — RCM (reverse Cuthill–McKee), так как на практике обратная нумерация индексов позволяет получить большее преимущество, нежели использование прямого алгоритма CM. Сильными сторонами применения этих алгоритмов являются: высокая скорость работы вычислительного алгоритма, так как приходится решать систему, приближенную к диагональной; сильный прирост скорости алгоритмов решения при использовании технологии, такой как CUDA  

Ключевые слова: методы перенумерации конечно-элементной сетки, трёхмерное математическое моделирование, задачи теории упругости, метод конечных элементов, конечно-элементные сетки

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Введение

На сегодняшний день имеет место быстрое развитие вычислительных комплексов высокой производительности. Этот рост позволяет брать во внимание задачи всё большего объёма. Основным методом решения задач теории упругости остаётся метод конечных элементов (МКЭ). Для высокой точности решения требуется строить довольно мелкую сетку по пространству. Но решение систем линейных алгебраических уравнений (СЛАУ) для таких задач занимает всё больше времени, а, следовательно, логично предложить метод по упрощению матрицы для исходного СЛАУ, который снизит вычислительную затратность этого процесса.
Одним из способов решения этой проблемы является перенумерация узлов конечно-элементной (КЭ) сетки. Основные преимущества этого подхода:
1) Независимость от сложности исходной геометрии модели;
2) Отсутствие потерь точности при использовании;
3) Лёгкая встраиваемость в уже существующие алгоритмы решения задач упругости;
4) Возможность распараллеливания на несколько потоков.

2. Общий подход

Рассмотрим упругое тело, занимающее область, где  — размерность пространства. Построим на нём КЭ сетку любым подходящим методом, как известно, получим граф . Любой граф можно представить в виде матрицы смежности, причём если рёбра  графа не ориентированы, то, очевидно, матрица  будет симметричной относительно главной диагонали.
Задача состоит в следующем: дана разреженная матрица , симметричная относительно главной диагонали, необходимо перенумеровать узлы исходного графа  так, чтобы как можно ближе к оси симметрии концентрировались ненулевые элементы (другими словами, надо уменьшить профиль матрицы ). После чего требуется составить перестановку из вершин графа  и применить её к исходной расчётной КЭ сетке. Стоит помнить, с сеткой могу быть связаны другие сущности, относящиеся к этой задачи, например, граничные и начальные условия принято задавать на узлах КЭ сетки, а значит надо позаботиться и о их перенумерации.
Далее следуют шаги предусмотренные алгоритмом решения задачи. Данный подход очень полезен при решении задач больших деформаций, в которых существенно изменяется форма модели (задачи описаны в [9], [10]). При решении механических задач с большим количеством включений ([8]) или задач о композитных материалах ([6], [7]) нумерации не будет отражать геометрической особенности тела, соответственно этот подход будет необходим для ускорения процесса решения.

3. Описания работы алгоритмов

3.1. Алгоритм RCM

Алгоритм CM был разработан в 1969 году Elizabeth Cuthill и J. McKee, затем Alan George разработал его «обратную» модификацию [2]. Будем считать, что наша модель была единым целым, а значит и граф  имеет лишь одну компоненту связности. Алгоритм построит упорядоченный кортеж вершин, представляющий новую нумерацию вершин. В алгоритме нами будет использоваться вспомогательная структура данных — очередь, будем обозначать её. Особенностью очереди, является порядок добавления и извлечения элементов: первый, добавленный в неё элемент, будет извлечён первым; а последний — последним.

1. Возьмём узел наименьшей степени, который не был ранее добавлен в 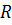, назовём его 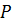. Добавим  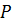на первую свободную позицию ;
2. Добавим в очередь 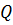 все узлы смежные с  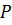узлы в порядке возрастания их степеней;
3. Возьмём первый узел из очереди 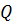, пусть это будет узел 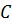. Если  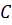ранее не был в 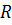, то добавим его в первую свободную позицию ;
4. Добавим в очередь 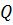всех соседей узла 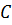, ранее не принадлежащих 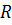, в порядке возрастания их степеней;
5. Если очередь 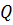 не пустая, то возвращаемся к шагу №3;
6. Изменяем порядок элементов кортежа 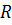 на обратный.

В итоге получаем перестановку , в которой на -ой позиции стоит номер узла (в старой нумерации), который в новой нумерации будет иметь номер . Если же исходное тело обладало несколькими компонентами связности, то этот алгоритм можно последовательно применить к каждой компоненте связности (а именно: перед переходом на шаг №6 переходить к шагу №1 последующей компоненты связности).

На самом деле результат работы данного алгоритма можно много улучшить, изменив правило поиска первого узла . Чтобы получить хороший результат, в качестве  нам понадобится периферийная вершина графа . Но эта задача для общего случая является вычислительно ёмкой, поэтому вместо неё будем искать псевдопериферийную вершину (используя модификацию эвристического алгоритма Гиббса [3]). В этом алгоритме используется понятие корневой структуры уровней: для заданной вершины  структурой уровней с корнем в вершинебудет разбиение  множества вершин:

Где подмножества определены следующим образом:

Где ;

Где ; ;  — множество смежности для.
Теперь опишем сам алгоритм:

1. Выбираем произвольную вершину 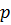 из множества всех вершин ;
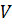2. Построим структуру уровней для корня : ;
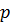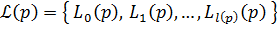3. Выберем вершину 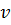 с минимальной степенью из множества;
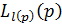4. Построим структуру уровней для корня :;
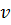
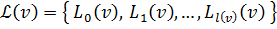5. Если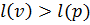, то присвоить вершине 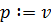и перейти к шагу №3;
6. Вершина 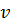 — искомая.

Таким образом, был описан алгоритм RCM для уменьшения профиля симметричных матриц, который с успехом можно применять к расчётным КЭ сеткам.

3.2.Алгоритм NodeND

NodeND был разработан George Karypis в 1995 году. Данный алгоритм основан на парадигме многоуровнего вложения разбиения, которая в свою очередь основана на алгоритме вычисления узла-разделителя для графа, соответствующего матрице [5]. Узлы-разделители перемещаются в конец матрицы, затем аналогичный процесс производится с каждой из двух полученных частей. Многоуровневая вложенная парадигма разбиения является достаточно эффективной для переупорядочения узлов, которое вытекает в матрицу с меньшим профилем. Этот алгоритм очень полезен, если при решении системы разреженных уравнений используется прямой метод. Полученная перестановка позволяет, как сократить время решения уравнения, так и уменьшить потребление памяти. Кроме того, это даст существенный выигрыш при параллельном использовании, так как достигается высокая степень параллелизма на этапе факторизации.
Но для использования NodeND, требуются низкоуровневые программные структуры созданные пользователем. Заполнение этих структур занимает дополнительное время, но не является вычислительно ёмким. Подробное описание этих структур можно найти в [4].

4.Результаты

RCM тратит много памяти на хранение графа сетки, фактически сетка хранится в памяти дважды, что плохо с точки зрения ресурсо-экономии. Сложность задачи построения графа равна; где  — количество элементов сетки,  — количество рёбер элемента. Другими словами, не экономный метод. NodeND же напротив, показывает очень хорошие результаты.
Тестирование проводилась на задачах статики, использовались тетраэдральные элементы. Рабочая станция обладала 16 GB оперативной памяти (этим обусловлено ограничение в размере задачи — 5 млн. элементов) и 4х ядерным процессором (использовалось ускорение, путём распараллеливания OMP). Наиболее заметный эффект наблюдается на задачах со сложной топологией тела или с большим соотношением сторон (то есть вдоль одной координаты тело очень вытянуто). Диаграмма 1 доказывает это утверждение.

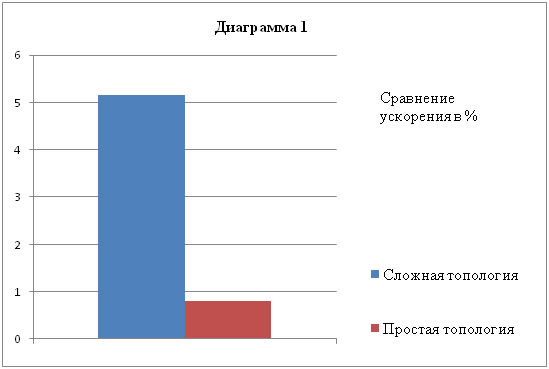
Стоит заметить, что перенумерация тратит значительно меньше памяти, нежели само решение, то есть если задача без перенумерации помещается в память, то и с перенумерацией поместится.
Далее приведён график 1, на котором отображено время, затрачиваемое на перенумерацию в зависимости от количества элементов.

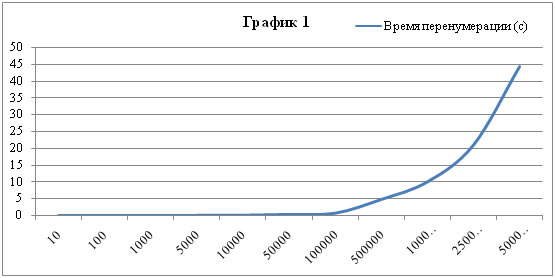
Стоит обратить внимание, что по оси абсцисс масштаб не линейный, но в таком масштабе лучше виден результат. Для сравнения ниже приведён этот же график 2 в логарифмическом масштабе.

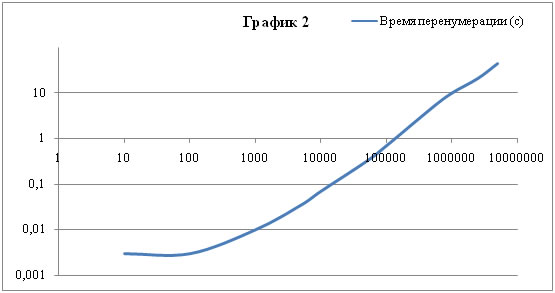
Если сравнить его с графиком 3, изображающим зависимость времени решения задачи (перенумерованной, без учёта времени перенумерации) от количества элементов, то видно, что перенумерация NodeND занимает не значительное время. Масштаб по всем осям логарифмический.

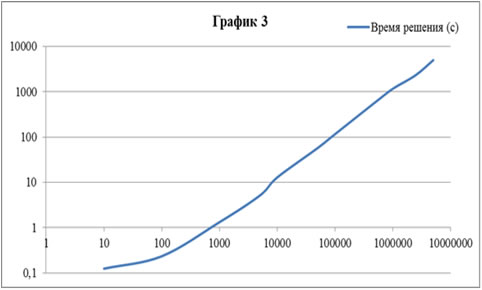
Но эти данные актуальны лишь при сравнении выигрыша от перенумерации и времени самой перенумерации (), график 4 приведён ниже.

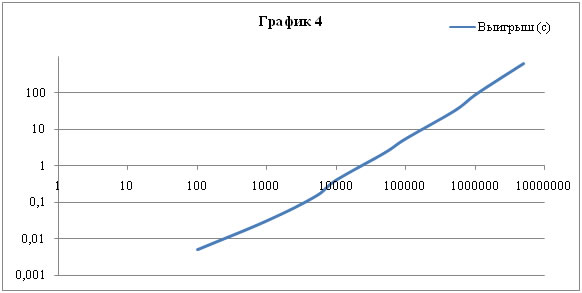
График 4 начинается не со значения 10 (элементов) по оси абсцисс, т.к. на таких малых задачах выигрыш отрицательный, соответственно, его не изобразить на логарифмической шкале.

1. 5.Заключение

На основании проделанной работы можно сказать, что перенумерация как таковая имеет смысл лишь при размере задач более 1 миллиона элементов. На графике 5 ниже приведено ускорение от перенумерации (с учётом времени на перенумерацию).

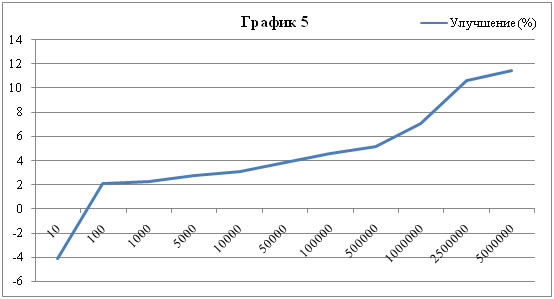
Выход из отрицательной зоны происходит уже на уровне 100 элементов, что значит, что перенумерация приносит пользу уже и на таких задачах (пусть незначительную).

Работа выполнена при финансовой поддержке Минобрнауки России по  государственному контракту от 15.06.2012 г. No. 07.524.11.4019 в рамках  ФЦП "Исследования и разработки по приоритетным направлениям развития  научно-технологического комплекса России на 2007-2013 годы".

Список литературы:

1. Ю.В.Василевский, А.А.Данилов, К.Н.Липников, В.Н.Чугунов. Автоматизированные технологии построения неструктурированных расчетных сеток (частное сообщение), 290 c.
2. Ciprian Zavoianu Tutorial: Bandwidth reduction - The CutHill-McKee Algorithm [Электронный ресурс] // Ciprian Zavoianu – weblog, January 15, 2009 http://ciprian-zavoianu.blogspot.ru/2009/01/project-bandwidth-reduction.html
3. Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений. — Москва.: Мир, 1984. — 333 с.
4. George Karypis METIS: A Software Package for Partitioning Unstructured Graphs, Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices Version 5.1., August 4, 2011, Department of Computer Science & Engineering University of Minnesota Minneapolis, MN 55455, 34 p.
5. G. Karypis and V. Kumar. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM Journal on Scientific Computing (pp. 359 — 392), 1999, 34 p.
6. Польской П.П., Маилян Д.Р. Композитные материалы – как основа эффективности в строительстве и реконструкции зданий и сооружений [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2009/1307 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Н.Е. Стёпин Реализация и сравнение различных вариантов алгоритма Узавы в задачах упругости для несжимаемых материалов [Электронный ресурс] // «Инженерный вестник Дона», Номер 2, 2013 г. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1626 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Левин В.А., Левитас В.И., Лохин В.В., Зингерман К.М., Саяхова Л.Ф., Фрейман Е.И. Твердотельные фазовые переходы, вызванные действием механических напряжений в материале с наноразмерными неоднородностями: модель и вычислительный эксперимент // Доклады РАН. 2010. Т. 434, № 4. c. 481-485
9. V. A. Levin, K. M. Zingerman.  A class of methods and algorithms for the analysis of successive origination of holes in a pre-stressed viscoelastic body. Finite strains// Communications in Numerical Methods in Engineering. 2008. V. 24. Issue 12. P. 2240-2251
10. Зингерман К.М.,  Левин В.А. Обобщение задачи Ламе-Гадолина для больших деформаций и ее аналитическое решение//  Прикладная математика и механика. 2013. Т. 77, вып. 2, с. 322-336