Прочностной расчет блока составной конструкции из шестиугольной пластины, круговой цилиндрической оболочки и отбортовки
Аннотация
Дата поступления статьи: 30.04.2013Статья посвящена прочностным расчетам составных конструкций. В основе положен ва-риационно-энергетический принцип. Рассмотрен расчет напряженно-деформированного состояния конструкции, состоящей из основания в форме шестиугольной пластины, жест-ко связанной с основанием круговой цилиндрической оболочки.
Ключевые слова: пластина, оболочка, вариационно-энергетический принцип, прочность, составная конструкция.
Конструкция состоит из ряда идентичных блоков, скрепленных друг с другом. Каждый такой блок состоит из основания в форме шестиугольной пластины, жестко связанной с основанием круговой цилиндрической оболочки, верхний торец которой усилен шестиугольной отбортовкой. Скрепление блоков друг с другом произведено с одной стороны по вершинам шестиугольных пластин, а с другой – по соответствующим вершинам отбортовок.
Толщины, как пластинки, так и цилиндрической оболочки достаточно малы, поэтому к ним при построении теории применима гипотеза Кирхгоффа-Лява, кольцеобразная шестиугольная отбортовка рассмотрена как стержень, деформируюшийся совместно с верхним краем цилиндрической оболочки. Материал блока принят упругим, однородным, изотропным. Внешняя нагрузка считается приложенной в вершинах шестиугольных пластин оснований. Для решения задачи используется известный вариационно-энергетический метод, состоящий в подсчете потенциальной энергии деформации и работы, производимой внешним нагружением и доставлении величине энергии минимума, соответствующего действительным перемещениям [1]–[10]. Из составной конструкции вырежем отдельный блок, причем заменим воздействие со стороны других блоков эквивалентной системой сил. Далее будет рассмотрен метод, с помощью которого завершается переход от одного блока ко всей конструкции. Для простоты сначала рассмотрим тот случай, когда нагрузка приложена в точке Аi – одной из вершин шестиугольного основания и в точке Вi – вершине шестиугольной отбортовки, соответствующей точке Аi, ( i=1,2,..,6 ), причем, случай симметричного нагружения рассмотрим отдельно. Таким образом, рассмотрим один вырезанный из всей конструкции блок. Поскольку даже отдельный блок является достаточно сложной конструкцией, рассмотрим его составные части.
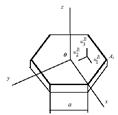
Рассмотрим нижнее основание блока (рис. 1), т.е. шестиугольную пластину и свяжем с ней прямоугольную декартовую систему координат x, y, z. В дальнейшем присвоим пластине номер I и перемещения вдоль осей x, y, z от некоторой нагрузки pi ( i=1,2,..,6 ), приложенной в одной из вершин Аi и соответствующей ей вершине Вi шестиугольной отбортовки, обозначим соответственно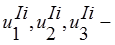 
индекс внизу обозначает номер координатной оси, первый индекс вверху – номер тела, второй – номер нагрузки (рис. 1).
 |
 |
| Рис. 1. – Шестиугольная пластина толщиной h |
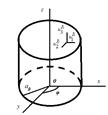
Рис. 2. – Круговая цилиндрическая оболочка толщиной H |
Выберем для пластины (тела I) некоторую аппроксимирующие функции, удовлетворяющие геометрическим условиям закрепления. Для данного случая такими являются равенство нулю перемещений во всех вершинах телаI, кроме той, где приложена нагрузка, а также учтем, что любую нагрузку можно представить в виде симметричной относительно оси x и кососимметричной. Кроме того, аппроксимирующие функции должны отражать характер изменения перемещений. Аппроксимирующие функции принимают вид: а).симметричное нагружение некоторого узла А1(тела I):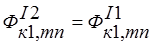 
; 
;
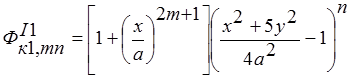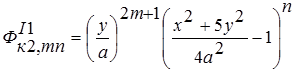; (1) 
; 
; 
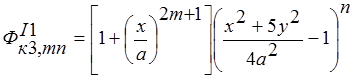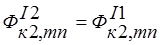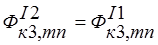; (2)
б).кососимметричное нагружение: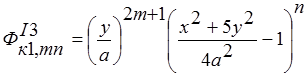 
;
;
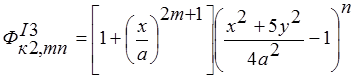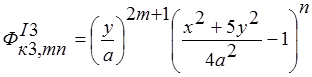; (3)
в).симметричное нагружение некоторого узла В1 (тела III) :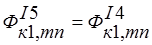 
; 
;
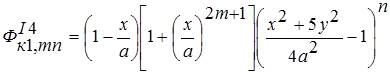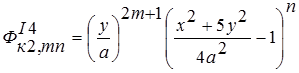; (4)
;
;
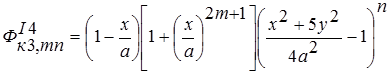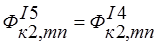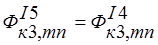; (5)
г).кососимметричное нагружение: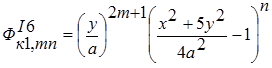 
;
;
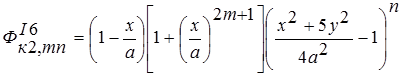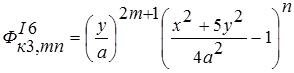. ( 6)
Подставим перемещения любой к-ой точки тела в виде разложений в ряды по выбранным аппроксимирующим функциям: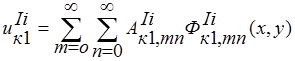 
;
;
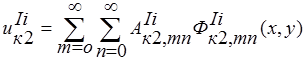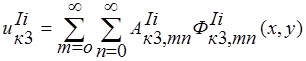,i=1,2,..,6 (7)
В общем случае тело I работает как на изгиб, так и на двустороннее растяжение. В таком случае энергия деформации записывается в виде выражений:
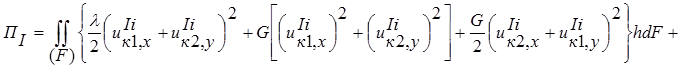
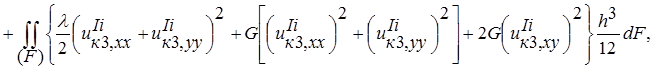(8)
где λ, G – упругие постоянные материала, h –толщина пластинки.
Рассмотрим цилиндрическую оболочку (тело II), введем цилиндрическую систему координат φ, r, z от (рис. 2), где радиус r отсчитывается от оси цилиндра, z – от торца, соединенного пластиной к торцу, усиленному шестиугольной отбортовкой. Для пластины выберем аппроксимирующие функции для перемещений, удовлетворяющие тем же условиям. В таком случае перемещения любой точки тела II от действия некоторой нагрузки равны:
;
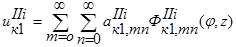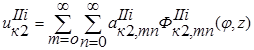
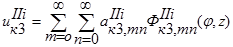. (9)
Проведя рассуждения, аналогичные изложенным в п.1.2 аппроксимирующие функции для тела II можно записать в виде:
;
;
; 
;
; 
; 
;
; 
;
; 
;
;
; 
; 
; 
; 
; 
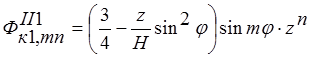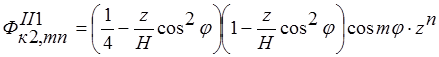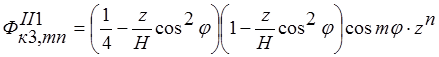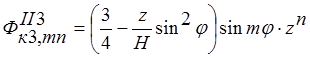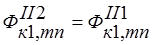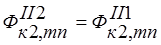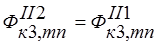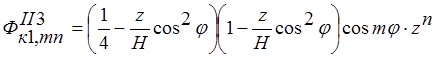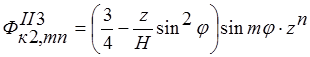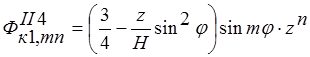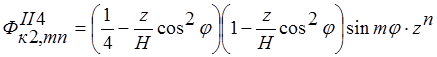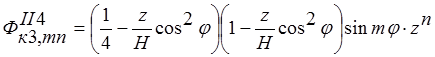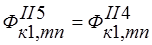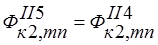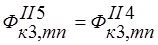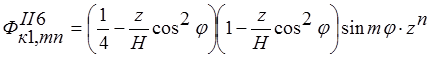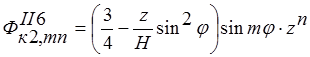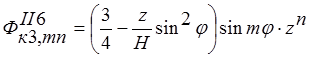. (10)
Можно записать энергию деформации тела II:
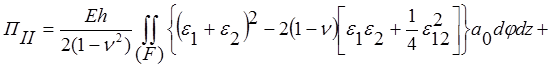
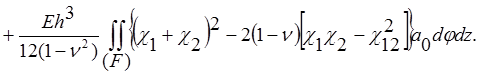, где деформации равны:
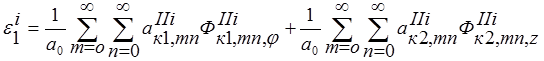; i=1,2,..,6
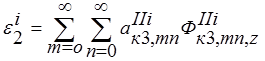
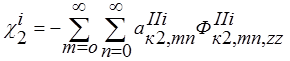
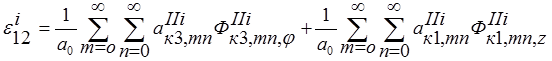
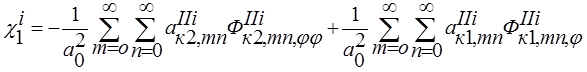
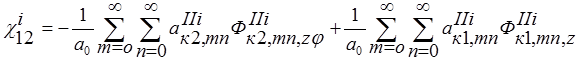(11)
Литература
1. Краснобаев И.А., Маяцкая И.А. Основы расчета на изгиб тонких жестких пластин [Текст]: Монография / Краснобаев И.А., Маяцкая И.А. – Ростов н/Д, РГСУ, 2011.– 87 с.
2. Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. Теория пластин и оболочек: [Текст]: Монография / Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. – Ростов н/Д, РГСУ, 2011.– 114 с.
3. Амосов А.А. Техническая теория тонких упругих оболочек: [Текст]: Монография / Амосов А.А.–М.:АСВ, 2009, – 332 с.
4. Филин А.П. Элементы теории оболочек.–Л.:Стройиздат, 1975, – 256 с.
5. Огибалов П.М., Колтунов М.Л. Оболочки и пластины.–М.:МГУ, 1969, – 696 с.
6. Calladine C.R. Theory of shell structures.– N.Y.: Cambridge University Press, 1989, –788 p.
7. Zingoni A. Shell structures in civil and mechanical engineering.– N.Y.: Thomas Telford Publishing, 1997, –351 p.
8. Новожилов В.В., Черных К.Ф., Михайловский Е.И. Линейная теория тонких оболочек.–Л.:Политехника, 1961, – 658 с.
9. Математическое моделирование. [Текст]: Монография/ Дж. Эндрюс, Р. Мак – Лоун. – М.: Мир, 1979.
10.Литвинов В.В., Кулинич И.И. Соотношения между компонентами поверхностной нагрузки в оболочках вращения при безмоментном их состоянии.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.
11.Стрельников Г.П., Бурцева С.В., Авилкин В.И. К расчету оболочек вариационно-энергетическим методом.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.