Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали
Аннотация
В данной работе изложен аналитический метод определения параметров трехпараметрического закона Вейбулла для совокупности конечного объема на основе параметров, полученных по выборке.
Представлен алгоритм расчета, по которому произведен вычислительный эксперимент.
На основании этих расчётов сделан вывод о том, что данным аналитическим методом следует определять параметры трехпараметрического закона Вейбулла для совокупности конечного объема на основе параметров, полученных по выборке.
Ключевые слова: совокупность конечного объема, выборка, дисперсия, среднее квадратическое отклонение, параметры распределения, прочность стали.Ключевые слова:
05.05.04 - Дорожные, строительные и подъемно-транспортные машины
В настоящее время основной задачей машиностроительной области является повышение надежности строительных машин. Для этого необходимо повышать гамма-процентный ресурс Трγ. Но расчетный ресурс по выборочным данным может быть весьма завышен. При этом объемы совокупности конечного объема (далее совокупность) могут составлять сотни тысяч машин. Такое количество объектов исследовать невозможно, поэтому предложен метод перехода от параметров выборочного распределения к параметрам распределения совокупности для трехпараметрического закона Вейбулла.
Этод метод предполагает переход от среднего значения выборочных дисперсий к дисперсии генеральной совокупности конечного объема[1]
![]() (1)
(1)
Методом максимального правдоподобия найдены выборочные параметры масштаба, формы и сдвига для закона распределения Вейбулла.
Среднее квадратическое отклонение для совокупности
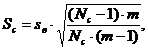 (2)
(2)
где sв – среднестатистическое отклонение для выборки [2]
![]() (3)
(3)
Коэффициенты gb и Kb [2]
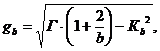 (4)
(4)
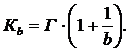 (5)
(5)
Тогда
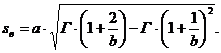 (6)
(6)
Аналогичные коэффициенты и соотношения для генеральной совокупности
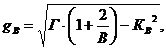 (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() , тогда получили уравнение
, тогда получили уравнение
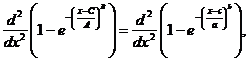 (10)
(10)
и ограничили искомые параметры неравенствами
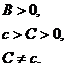 (11)
(11)
Система неравенств с учетом вышеперечисленных коэффициентов и зависимостей
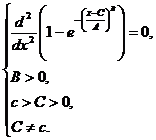 (12)
(12)
Используя зависимости (2-12), получен аналитический метод и составлен алгоритм расчета параметров распределения закона Вейбулла А, В, С для совокупности, представленный на рис.1.
Принятые в данном алгоритме обозначения: хi – вариационные ряды; а, b, с – выборочные параметры масштаба, формы и сдвига закона Вейбулла; А, В, С – аналогичные параметры совокупности.

Рис.1. Алгоритм расчета параметров распределения закона Вейбулла А, В, С для совокупности
По данному алгоритму проведен вычислительный эксперимент. Из моделированной совокупности,например объемом Nс=104 получены выборки объемом m=50;100 в количестве n=100 (в таблице 1 представлено по 10 вариантов). Определены параметры распределения совокупности Аi, Вi, Сi для каждой выборки, найдены гамма-процентные значения для сдвигов выборки сγ и совокупности Сγ., а также разница между ними,которая составляет для m=50 Δ=1,11÷10,89, а для m=100Δ=0,97÷8,08 (таблица).
Таблица
Исходные данные и результаты расчета распределения трехпараметрического закона Вейбулла
|
m |
Nc |
a |
b |
с |
A |
B |
C |
Сγ |
сγ |
ΔСγ , % |
|
50 |
|
21.09 |
2.71 |
125.92 |
36.02 |
4.53 |
111.46 |
118.99 |
127.57 |
7.21 |
|
18.18 |
2.04 |
129.20 |
36.31 |
4.00 |
112.17 |
118.64 |
129.82 |
9.42 |
||
|
38.21 |
5.03 |
113.23 |
38.4 |
4.58 |
113.07 |
121.56 |
122.91 |
1.11 |
||
|
15.00 |
1.83 |
130.21 |
36.26 |
4.38 |
110.25 |
117.73 |
130.55 |
10.89 |
||
|
34.05 |
4.20 |
115.90 |
39.90 |
4.80 |
110.21 |
119.68 |
122.48 |
2.34 |
||
|
21.02 |
2.92 |
126.28 |
33.53 |
4.60 |
114.24 |
121.71 |
128.25 |
5.37 |
||
|
29.30 |
3.45 |
119.85 |
37.07 |
4.30 |
112.36 |
119.80 |
123.81 |
3.35 |
||
|
26.11 |
3.50 |
120.44 |
35.71 |
4.79 |
111.15 |
119.59 |
124.07 |
3.75 |
||
|
32.24 |
3.95 |
115.70 |
36.38 |
4.34 |
111.71 |
119.12 |
121.31 |
1.84 |
||
|
26.54 |
2.98 |
121.69 |
38.03 |
4.28 |
110.68 |
118.24 |
124.30 |
5.13 |
||
|
100 |
104 |
33.12 |
4.30 |
114.86 |
37.85 |
4.93 |
110.25 |
119.58 |
121.50 |
1.61 |
|
28.65 |
3.4 |
119.58 |
38.24 |
4.65 |
110.31 |
118.97 |
123.34 |
3.67 |
||
|
27.10 |
3.28 |
120.68 |
37.29 |
4.41 |
110.85 |
118.63 |
123.98 |
4.51 |
||
|
28.34 |
3.38 |
120.41 |
38.01 |
4.28 |
111.063 |
119.01 |
124.08 |
4.26 |
||
|
36.36 |
4.57 |
111.92 |
37.76 |
4.53 |
110.56 |
118.79 |
119.94 |
0.97 |
||
|
30.62 |
3.95 |
116.50 |
36.96 |
4.49 |
110.34 |
118.30 |
121.83 |
2.98 |
||
|
29.51 |
3.82 |
118.60 |
36.97 |
4.69 |
111.36 |
119.83 |
123.44 |
3.01 |
||
|
21.57 |
2.42 |
125.25 |
37.49 |
4.09 |
110.11 |
117.03 |
126.49 |
8.08 |
||
|
29.74 |
3.87 |
118.41 |
37.80 |
4.82 |
110.57 |
119.59 |
123.40 |
3.19 |
||
|
27.74 |
3.45 |
120.96 |
38.86 |
4.88 |
110.18 |
119.63 |
124.71 |
4.25 |
По данным таблицы (строка *) построен график (рис.2) плотностей распределения трехпараметрического закона Вейбулла.
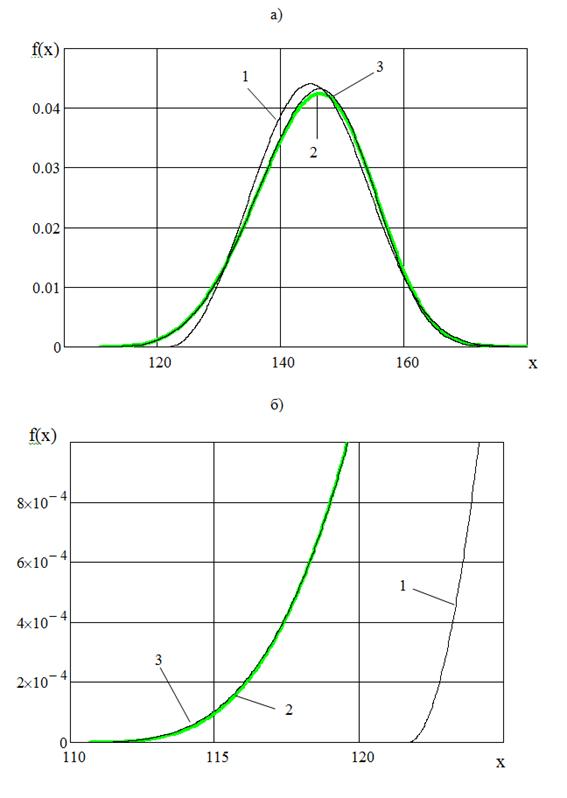
Рис.2(а,б) Плотности распределения трехпараметрического закона Вейбулла: 1 – по выборочным данным ʄ(x, a, b, c), 2 – по найденным по алгоритму (рис.1) параметрам для совокупности ʄ(x, A, B, C), 3 – по параметрам исходной совокупности ʄ(x, Aс, Bс, Cс); Cγ и cγ- гамма-процентное значение параметра сдвига соответственно для совокупности и выборки (γ = 99,999%); с, С – параметр сдвига для выборки и совокупности по алгоритму (рис.1). Таким образом, можно сделать вывод о том, что аналитическим методом следует определять параметры трехпараметрического закона Вейбулла для совокупности конечного объема на основе параметров, полученных по выборке.
Список литературы:
1. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648с.
2.ГОСТ 11.007-75. Прикладная статистика. Правила определения оценок и доверительных границ для параметров распределения Вейбулла. М.: Изд-во стандартов, 1975. - 30 с.