Метод гибкого формирования подсистемы частотно-временной локализации сигналов в задачах адаптивной фильтрации

Аннотация

А.Ю. Линович

Дата поступления статьи: 27.02.2014

Представлен новый подход к построению многоступенчатых подсистем частотно-временной локализации сигналов. Проведённые исследования ограничены классом цифровых цепей с конечной импульсной характеристикой.
Приводится пример, поясняющий методику согласования пирамидальной структуры, образованной многоступенчатым включением некоторой простой подсистемы анализа-синтеза, с характеристиками выбранного канала связи. Описанная методика позволяет выполнить более точную локализацию входного сигнала в отдельных частотных диапазонах. Адаптивное формирование структуры частотно-временного преобразования позволяет улучшать показатели, характеризующие эффективность многоскоростных адаптивных фильтров (МАФ).
Применение метода гибкого формирования подсистемы частотно-временной локализации сигналов в задачах адаптивной фильтрации позволяет значительно снизить вычислительные затраты на реализацию МАФ в реальном времени.
Другое важное достоинство гибкого формирования МАФ на основе алгоритма наименьших средних квадратов заключается в сокращении времени настройки адаптивной системы.

Ключевые слова: адаптация, фильтр, многоскоростной, сигнал, частотно-временной

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Введение

Важными задачами адаптивной фильтрации, получившими широкое распространение в цифровой обработке сигналов, являются задача прямого и обратного моделирования, а также задача шумоподавления. Общую постановку и методы решения этих задач можно найти в [1, 2]. Другим не менее важным направлением цифровой обработки сигналов является многоскоростная обработка, основы которой были подробно рассмотрены ещё в [3, 4]. Оба указанных выше направления цифровой обработки сигналов во многом дополняют друг друга. Оба направления активно развиваются в настоящее время, о чём свидетельствуют [5, 6], а также многочисленные публикации в периодических изданиях, например: [7 — 11]. Совместное использование методов адаптивной и многоскоростной обработки сигналов позволяет повысить эффективность адаптивных систем.
Классическая структура [6] многоскоростного адаптивного фильтра (МАФ) рассмотрена на рис. 1. На этой схеме предполагается, что МАФ используется в составе эквалайзера, устраняющего внесённую каналом связи межсимвольную интерференцию и размещённого в модеме, принимающем сигнал с одной несущей частотой.
В отличие от обычного адаптивного фильтра (АФ), принимаемый модемом сигнал  и эталонная последовательность настройки  предварительно разбиваются подсистемой анализа на  частотных каналов. Благодаря тому, что спектр сигнала в каждом канале занимает лишь часть исходной полосы частот, появляется возможность понизить частоту дискретизации в  раз (). Настройка адаптивных фильтров выполняется на пониженной частоте дискретизации, что позволяет существенно снизить вычислительные затраты на реализацию МАФ в реальном времени (при относительно высоких порядках МАФ), а также повысить скорость процесса адаптации при использовании ряда широко известных адаптивных алгоритмов [7].

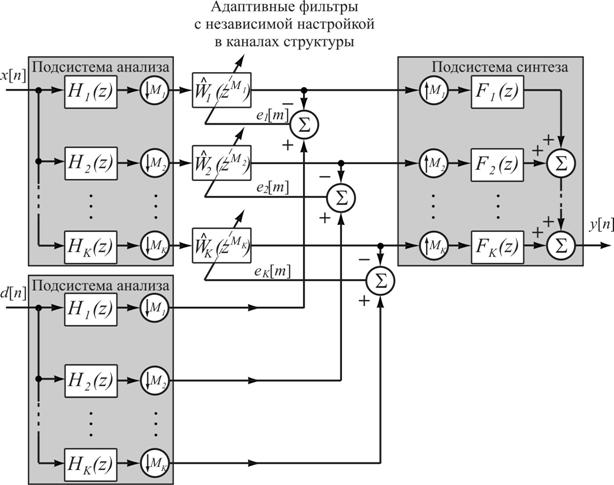
Рис. 1. Классическая структура МАФ (применительно к задаче обратного моделирования)

Теоретическое исследование
В данной статье проводится исследование многоступенчатых подсистем частотно-временной локализации сигналов. При многоступенчатом использовании одной простой подсистемы анализа-синтеза можно получить так называемую пирамидальную структуру, которую в дальнейшем нетрудно согласовать с характеристиками выбранного канала связи для получения более детальной локализации входного сигнала в отдельных частотных диапазонах. В результате, появляется возможность адаптивно формировать структуру частотно-временного преобразования и тем самым дополнительно улучшать показатели, характеризующие эффективность МАФ [8 – 9].
В дальнейших рассуждениях ограничимся классом цепей с конечной импульсной характеристикой. В этом случае можно считать, что точность восстановления сигнала на выходе МАФ определяется длиной воспроизводимой им импульсной характеристики. При равной длине импульсных характеристик (порядок эквивалентного широкополосного фильтра равен ) получаем следующие расчётные соотношения для оценки вычислительных затрат (см. табл. 1).

Таблица 1

В табл. 1 содержатся формулы расчёта вычислительных затрат для МАФ на основе нормированного алгоритма среднеквадратического отклонения (НСК). В зарубежной литературе данный алгоритм наиболее популярен и носит название «normalized least-mean-square (NLMS) algorithm» [6]. Предполагается, что подсистема анализа-синтеза состоит из одной ступени анализа и одной ступени синтеза.  — вычислительные затраты, связанные с введением подсистемы анализа-синтеза и оценённые в среднем числе операций вещественного умножения-накопления на один отсчёт входного сигнала. Точные значения , указанные в табл. 1, найдены в предположении, что для построения подсистемы анализа-синтеза используется метод расчёта, описанный в [10].
Экспериментальное исследование
Пример гибкого подхода к формированию структуры МАФ рассмотрен на рис. 2. В данном эксперименте использован МАФ, эквивалентный порядок которого  = 1200. Здесь дважды используется одна и та же трёхканальная подсистема анализа-синтеза.

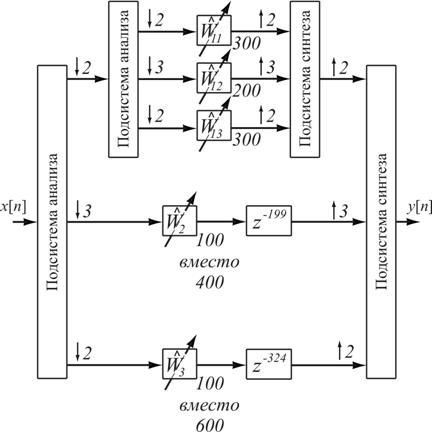
Рис. 2. Пример адаптивного подхода к формированию структуры многоканального адаптивного фильтра (вторая подсистема анализа для упрощения не показана)

Такой МАФ оказывается эффективным в тех случаях, когда наиболее сильные искажения сосредоточены в низкочастотном диапазоне (этому диапазону соответствует верхняя часть структуры). Для низких частот выполняется повторное разбиение сигнала по частоте, а для остальных достаточно однократного разбиения входного сигнала . Кроме того, в тех случаях, когда искажения, внесённые в сигнал , для диапазонов средних и верхних частот оказываются незначительными, можно понизить порядки адаптивных ядер, установленных в этих каналах МАФ, что позволяет получить дополнительную экономию по вычислительным затратам.
Более наглядно эффект экономии вычислительных затрат, достигаемый при использовании многоступенчатой структуры подсистемы анализа-синтеза за счёт применения метода гибкого формирования подсистемы частотно-временной локализации сигналов, отражён на рис. 3.

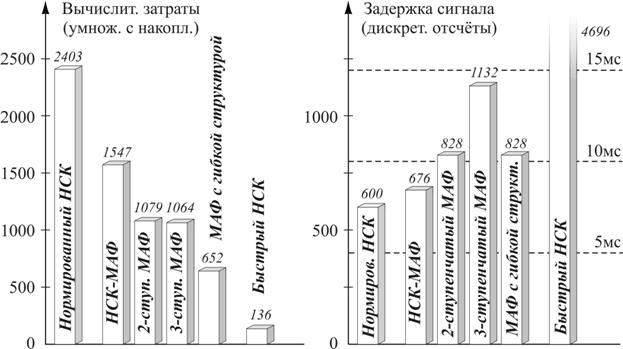
Рис. 3. Сравнение эффективности различных адаптивных структур:
слева — вычислительные затраты, справа — задержка в обработке

С ростом числа ступеней разбиения входного сигнала должен сокращаться объём вычислительных затрат на построение МАФ (при равной точности настройки). Но на практике, уже начиная с 4-ступенчатой структуры, этот эффект перестаёт наблюдаться в связи с увеличением затрат на реализацию усложняющейся подсистемы анализа-синтеза.
Справа на рис. 3 сравниваются задержки, вносимые различными адаптивными структурами. Введение подсистем анализа-синтеза увеличивает задержку, вносимую МАФ (при равной точности настройки, определяемой длиной воспроизводимой адаптивным фильтром импульсной характеристики). Для большего удобства указаны значения задержки в миллисекундах, вычисленные для модемов стандарта V.90.
Столбец диаграммы, получивший наименование «МАФ с гибкой структурой», соответствует структуре, изображённой на рис. 2. Как видим, гибкий подход к формированию структуры МАФ заметно повышает конкурентоспособность такого рода структур по сравнению с адаптивными фильтрами, работающими во временной («НСК») и частотной («Быстрый НСК») областях. Быстрый алгоритм НСК имеет значительное преимущество по вычислительным затратам, однако имеет серьёзный недостаток, связанный с большой задержкой в обработке сигнала, вызванной выполнением дискретного преобразования Фурье.

Выводы

Благодаря применению метода гибкого формирования подсистемы частотно-временной локализации сигналов в задачах адаптивной фильтрации, удаётся значительно снизить вычислительные затраты на реализацию МАФ. Перспективные исследования в данном направлении связаны с применением подобных МАФ в системах типа [11, 12].
Ещё одним достоинством МАФ на основе алгоритма НСК, не нашедшим отражения на приведённых здесь иллюстрациях, является повышение скорости настройки.

Литература:

1. Уидроу Б., Стирнз С. Адаптивная обработка сигналов [Текст] / пер с англ. – М.: Радио и связь, 1989. – 440 с.
2. Адаптивные фильтры [Текст] / пер. с англ. под ред. К.Ф. Коуэна и П.М. Гранта. – М: Мир, 1988. – 392 с.
3. Витязев В.В. Цифровая частотная селекция сигналов [Текст]. – М: Радио и связь, 1993. – 240 с.
4. Crochiere R.E., Rabiner L.R. Multirate Digital Signal Processing [Текст]. – NJ: Prentice-Hall, 1983. – 411 pp.
5. Harris F.J. Multirate Signal Processing for Communication Systems: Current Practice and Next Generation Techniques [Текст]. – NJ: Prentice-Hall, 2004. – 496 pp.
6. Haykin S. Adaptive Filter Theory [Текст]. – London: Pearson, 5th ed., 2013. – 912 pp.
7. Harteneck M., Weiss S., Stewart R.W. Design of near perfect reconstruction oversampled filter banks for subband adaptive filters [Текст] // IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process. – 1999. – Vol. 46. – pp. 1081–1085.
8. Линович А.Ю. Многоканальный эквалайзер на основе субполосной адаптивной фильтрации [Текст] // Международная научно-техническая конференция «Цифровая обработка сигналов и её применение»: Тезисы докладов. – 2007. – Т.1. – С. 89–92.
9. Линович А.Ю. Эквалайзер с адаптивной многоканальной структурой [Текст] // Международная научно-техническая конференция «Цифровая обработка сигналов и её применение»: Тезисы докладов. – 2010. – Т.1. – С. 56–59.
10. Harteneck M., Weiss S., and Stewart R.W. Design of Near Perfect Reconstruction Oversampled Filter Banks for Subband Adaptive Filters [Текст] // IEEE Transactions on Circuits & Systems II. – 1999. – Vol. 46. – pp. 1081–1086.
11. Линович А.Ю. Динамический выбор порядка в многоскоростном адаптивном фильтре [Электронный ресурс] // «Инженерный вестник Дона», 2013, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2013 /2002  (доступ свободный) – Загл. с экрана. – Яз. рус.
12. Колесников С.В., Зайцева Т.В., Рогожкина А.Ю., Ушаков С.А., Комиссаров А.В. Влияние пространственной структуры активной антенной решетки на угловые спектры мощности интермодуляционных помех [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4, ч. 2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1468  (доступ свободный) – Загл. с экрана. – Яз. рус.