Анализ сборки насоса с учетом статики

Аннотация

И.К. Рыльцев, И.С. Храмов

Дата поступления статьи: 23.12.2013

Рассматривается конструктивная особенность насоса и представлены результаты исследования отдельных сборочных деталей насоса: вала со  шпонками и  рабочих колес. Исследование включало: измерение биения вала  и вала с рабочими колесами, на основании измерений сделано заключение. 

Ключевые слова: сборка, вал, колесо, анализ, биение, зазор.

05.02.08 - Технология машиностроения

В последние годы в России ведется активный поиск путей повышения эффективности использования сырьевых, интеллектуальных, финансовых, кадровых и других ресурсов страны, способствующих модернизации российской   экономики [1, 2].
Анализ и изучение вероятностных характеристик    событий, а также оценка надежности действия технических   систем относительно теории надежности. Обычно под     надежностью понимается способность изделия (элемента,         сооружения, системы) выполнять в определенных условиях     эксплуатации все заданные функции, сохраняя рабочие           параметры в пределах установленных допусков, в течение     требуемого интервала времени [3]. Надежность работы механизма зависит не только от эксплуатации, но и от деталей из   которых он состоит. Конструкция насоса ЦНСн сложная, сборка содержит большое количество деталей, при сопряжении          которых образуются натяги и зазоры [4]. Есть зазоры которые невозможно проконтролировать в процессе сборки. Один из   таких является зазор между    колесом и корпусом насоса,       который при сопряжении деталей должен находиться в пределах 0,30-0,35мм. Этот зазор является щелевым уплотнением,       применяемое для уменьшения перетекания жидкости из области положительного      давления в область всасывания с внешней стороны рабочего колеса. В общем случае щелевое уплотнение представляет собой цилиндрическую щель, образованную неподвижной деталью - кольцом 5, корпуса насоса 4 и вращающимся рабочим колесом 2, установленном на валу 1.    Герметизирующая способность зависит от зазора между вращающимися деталями, который хотя и устанавливается    минимально возможным, чтобы исключить их трение, но вызывает значительные потери напора (давления) в щели [5]. Чем      больше путь протекания жидкости в зазоре L, тем надёжнее уплотнение рис. 1.

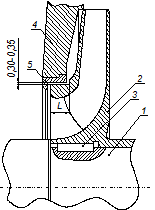
Рис. 1. - Узел сборки насоса
1 –  вал; 2  – рабочее колесо; 3 – шпонка; 4 – корпус насоса;   5 – неподвижное уплотнительное кольцо

 Для гарантии качественной сборки, состоящих из двух слагаемых, которые связаны числом зазора между колесом 2 и неподвижным уплотнительным кольцом 4 в пределе 0,30-0,35мм, согласно конструкторскому чертежу. На практике при сборке проверить данный зазор нельзя, чтобы гарантировать качественную сборку произведем синтез тех деталей сборки,     которые влияют на этот зазор. Для условной вероятности исследования произведем синтез узловой сборки вала с колесами [6].
Базовой деталью является вал, на который устанавливаются рабочие колеса на шпонках. Анализирую можно отметить, что каждая деталь: вал и колесо имеют свою центральную ось параметра симметрии. Очень важно при сборки чтобы однозначно  оси сопрягаемых деталей совпадали при этом можно проследить траектории при движении колес на валу. Установим вал в центра и произведем измерения. Для более точного анализа возьмем в каждом рассматриваемом сечении 36 точек, которые будут проходить через равнозначные углы φº =10º. Измерения производим индикатором часового типа с ценой деления 0,01 мм.
Анализ геометрии вала
Базовая деталь насоса – вал. Рассмотрим на валу 10 сечений (ceч) и  сделаем промеры биения R мм, поворачивая вал на угол φº=10º, произведем измерение 36 точек за один оборот вала.
Для наглядности построим диаграмму суммарных значений биения точек вала по сечениям, чтобы лучше    проанализировать, как изменяется биение в каждом сечении в числовом диапазоне  [7].

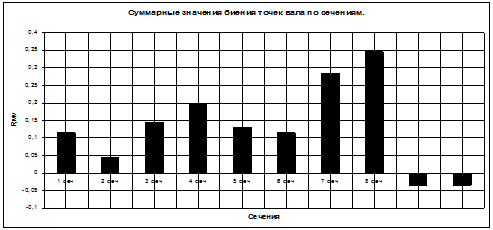
Рис. 2. - Диаграмма суммарных значений биения точек вала по сечениям.

Из результатов диаграммы выделяется сечение № 8 имеющие суммарное максимальное положительное биение и отрицательное – это сечения № 9, 10. Можно предположить, что при установке рабочего колеса на вал в сечении № 8 биение    самого колеса увеличиться или уменьшиться, чтобы найти ответ произведем анализ сборке: вал, колесо и шпонка.

Анализ сборки: вал, колесо и шпонка
Рассмотрим сборку на 10 сечениях (ceч) и сделаем промеры биения R мм колес установленных на вал, поворачивая вал на угол φº=10º, построим диаграмму.

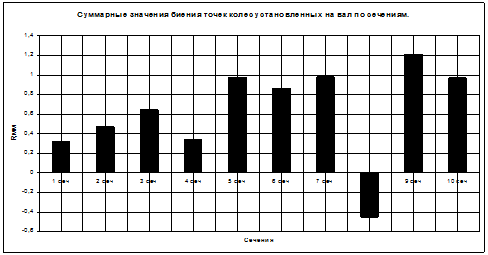
Рис. 3. - Диаграмма суммарных значений биения точек колес   установленных на вал по сечениям.

Из результатов диаграммы максимальное положительное суммарное биения точек колеса в сечении № 9, а отрицательное минимальное суммарное значение биения в сечении № 8. Если сравнить две диаграммы рис. 2, 3, то можно проанализировать, как изменяется биение в сечениях до установки рабочих колес и после. Фактически диаграмма рис.3 является результирующей в данной узловой сборке. По этой диаграмме можно сделать вывод, что в сечениях № 1, 2, 4 и 8 рабочие колеса установлены с наименьшей погрешностью, так как суммарные значения биения в этих сечениях ближе к нулю. Для того чтобы более точно рассмотреть правильность расположения колес на валу, определим смещение координат центров.
Результат таблицы № 1 и таблицы № 2 дают разные       показания измерений 36 точек за один оборот вала. Для наглядности определим смещения центров вала по формуле:
,  при   (1)                              
Также определим смещение центров сборки: вал (в), шпонка (ш), колесо (к) по формуле:
,  при  (2)                                
На основании полученных данных строим график. Приведем  криволинейную зависимость смещения центров от угла поворота в линейную [8]. Для этого при помощи программы       Microsoft Office Excel построим для графика линию тренда, эти линия и будет ось симметрии двух сопрягаемых деталей: вала и колеса.

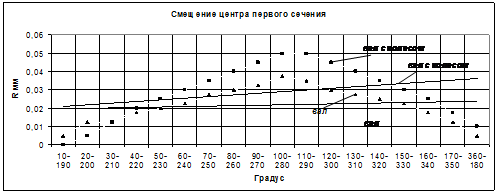
Рис. 4. - Графики измерения точек формы сборки:вала и колеса

Видно из графика, что кривые не совпадают. Далее можно определить значения углов между осью абсцисс и линией тренда как для вала и колеса на валу. Для этого введем обозначение
 – угол между осью абсцисс и линией тренда для окружности вала;
 – угол между осью абсцисс и линией тренда для   окружности вала с колесом.
Полученные данные по каждому сечению занесем в табл.1

Таблица № 1
Результаты анализа графиков по каждому сечению вала.

Как видно из таблицы, углы в сечениях разные, есть сечения, где  или наоборот , следовательно, зазор в     щелевом уплотнении при вращении будет изменяться, можно предположить, что рабочие колеса будут работать с разной     нагрузкой.
Для того чтобы с большей уверенностью предположить, что именно в данном сечении колесо работает с наименьшей погрешность. Cвяжем функцию плотности вероятности  случайной величины   независимых величин с       данными измерений точек вала и точке колес на валу [9].
, (3)              
где - сумма случайных  величин n-го сечения m-й значений, .
Случайные измерения точек радиусов , зависит от разности смещений центров    сечений вала и смещений центров сечений колес на валу , мм.                                                                                 
Полученные значения  плотности вероятности колес  на валу относительно шпонок на валу по функции (1)  и их отношений  [10] представим в  таблице № 2.
Таблица № 2

Результаты значений до поворота рабочих колес на валу.

Как видно из результатов плотности вероятности случайных величин таблицы № 2, наибольшее значение в 8-мом   сечении, это говорит о том, что в данном сечении ось рабочего колеса с большей вероятностью совпадает с осью вала.
Рабочие колеса в некоторых сечениях имеют низкую вероятность, следовательно, создают наибольшее биение. Для улучшения работы рабочих колес, найдем им такое положение, при котором будет наибольшая вероятность, следовательно, наименьшее биение. Для этого в тех сечениях, где значение вероятности  меньше 1, повернем колеса, на угол исходя из результатов графиков смещения центров, пытаясь найти такое положение колес, где построения  двух множеств точек совпадут, и произведем сравнение до поворота и после.
Рассмотрим сечения колес m= 2,3,4,5,6,7,9,10 на одном валу, сечения  колес m=1; 8 рассматривать не стоит, исходя из графиков смещения центров. Каждое колесо повернем до     максимального возможного совпадения измеренных двух множеств точек поверхностей деталей вала и узла колеса на валу.

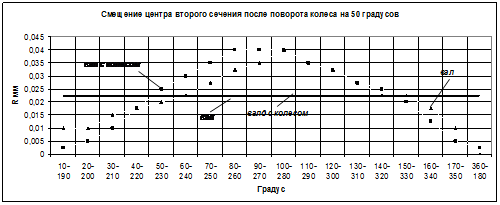
Рис. 5. - Графики измерения точек формы сборки: вала и колес

Произведем перерасчет, результат представим в таблице № 3 и произведем сравнения результатов до и после поворота колес в каждом сечении.

Таблица № 3

Результаты значений после поворота рабочих колес на валу.

 На основании проведенных замеров определены сечения, где рабочие колеса работают с наибольшей погрешностью с учетом статики. При первоначальном анализе сборке были     выделены сечения №1,2,4 и 8 на основании диаграмм рис. 2,3, где рабочие колеса установлены с наименьшей погрешностью. Диаграммы  суммарных значений биения не дают точного ответа. Для более точно ответа на этот вопрос были построены графики смещения координат центров. Из  графиков смещения координат центров видно, где оси рабочих колес не симметричны по отношению к оси вала это сечения № 2,3,4,5,6,7,9,10. На практике при дефектации данных деталей обнаруживаются различные дефекты, особенно это износ шпоночного паза на рабочем колесе и посадочной поверхности рабочего колеса на вал. В процессе ремонта центробежных насосов произвести контроль зазора в щелевом уплотнении не возможно из-за конструктивной особенности. Можно предположить, что зазор в щелевом уплотнении не всегда постоянен, исходя из результатов исследования. Следовательно, каждое рабочее колесо работает с разной нагрузкой, что приводит к неравномерному износу сопрягаемых поверхностей. Для предотвращения этого необходимо:
- производить дополнительный анализ сборки, в зависимости от сложности конструкции
- предположить наилучшее взаимное положение деталей в сборке, исходя из результатов анализа.
В данной сборке определили, что рабочие колеса в сечениях  №1,8 работают с минимальным риском отказа.
Для улучшения работы насоса повернем колеса в каждом сечении на определенный угол до совпадения графиков, в сечениях № 3,4,6,7,9,10 относительно часовой стрелки, а в сечениях № 2 и 5 против часовой стрелки. Как видно из результатов расчета плотности вероятности до и после поворота колес, можно с уверенность утверждать, что данное расположение колес на валу будет лучше влиять на их работоспособность и надежность, так как возможность возникновения максимального биения минимально, это следует из результатов расчета плотности вероятности.

Список литературы:

1. Демаков Д.В. Краткий анализ исследований проблем развития регионального машиностроения [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/979/ (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Valve World Americas Expo &Conference [Электронныйресурс] – Режим доступа: http://www.valveworldexpoamericas.com/ (доступ свободный)– Загл. с экрана. – Яз.англ.
3. Петренко С.Е. Параметры надежности эксплуатации насосных станций и мероприятия по их повышению [Электронный ресурс] // «Инженерный вестник Дона», 2010,  № 4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2010/256/ (доступ свободный) – Загл. с экрана. – Яз. рус.
4. HowValveManufacturersHelpMaintainGeothermalPowerPlants [Электронный ресурс] – Режим доступа: http://www.gwcvalve.com/news/industrynews.php (доступ свободный). – Загл. с экрана.– Яз.англ.
5. Белецкий Д.Г. Прогрессивная технология насосостроения М.: Машиностроение, 1969.-368 с.
6. Большев Л.Н., Смирнов Н.В.: Таблицы математической статистики. – М.: Наука. 1983.-416 с.  
7. Иориш Ю. И. Виброметрия: - М.: Государственное научно-техническое издательство машиностроительной   литературы, 1963. - 756 с.
8. Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: «Наука», 1968. – 512 с.
9. Закс Ш.. Теория статистических выводов. – М.: Мир, 1975.-776 c.
10. Большев Л.Н., Смирнов Н.В.: Таблицы математической статистики. – М.: Наука. 1983.-416 с.